Vigas de Concreto Armado: Guia Essencial sobre Flexão Simples

O mecanismo de flexão simples em vigas de concreto armado ocorre apenas com a ação do momento fletor, sem a presença do esforço normal, diferentemente da flexão composta, na qual eles atuam em conjunto.

Aliás, as vigas são submetidas, na maioria dos casos, à flexão normal simples, embora possam, em determinadas situações, também sofrer a ação de flexão composta.

Dito isso, compreender como esses esforços atuam e se distribuem é essencial para o dimensionamento seguro e eficiente das estruturas.

Portanto, vamos entender de forma simples e prática a flexão simples em vigas de concreto armado, com base na norma brasileira NBR 6118 2023.

Flexão simples em vigas de concreto armado

Então, a flexão simples em vigas caracteriza-se por diferentes etapas, denominadas de estádios, e representam a sua evolução sob a ação crescente de cargas.

Nestes casos, elas passam de uma situação bem íntegra e isenta de danos, o estádio I, para a formação crescente de fissuras, o estádio II, até chegar ao seu limite de resistência, ou seja, a ruptura no estádio III.

A propósito, no estádio III, a viga atinge o estado limite último (ELU), no qual todos os elementos estruturais, como vigas, lajes, pilares e fundações, são dimensionados.

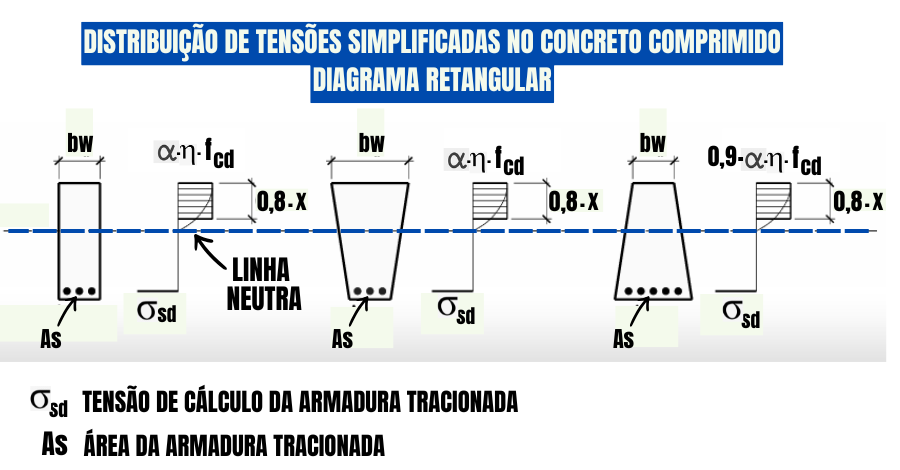
Neste estágio, o diagrama de tensões no concreto é não linear e adquire uma configuração semelhante a uma parábola mais retangular.

No entanto, segundo a NBR 6118 2023, pode-se substituir este diagrama por um simples retângulo com altura y igual a λ.x, onde:

• x – altura da linha neutra;
• λ=0,8: concretos com fck ≤ 50 MPa;
• λ = 0,8 – (fck – 50) / 400, para fck > 40 MPa;
• fcd = fck/४c, fcd é a resistência de cálculo do concreto, avaliada aos 28 dias ou mais de idade;
• ४c – coeficiente de minoração do concreto, na maioria dos casos, igual a 1,4;

Aliás, a norma brasileira também apresenta equações mais complexas para verificar a resistência à compressão do concreto (fcd) em idades inferiores a 28 dias.

Por outro lado, a tensão no concreto, ao longo da altura y do retângulo, assume um valor constante de:

• A– ∝c.ηc.fcd: quando a largura da seção (bw) mantém-se ou aumenta em direção à zona comprimida, medida paralelamente à linha neutra.
• B – 0,9 ∝c ηc fcd: caso contrário, a (A).;
• ∝c=0,85: com concretos de fck ≤ 50 MPa;
• ∝c = 0,85 – 1 – [(fck – 50) / 200]: fck > 50 MPa;
• ηc=1: fck ≤ 40 MPa;
• ηc = (40/fck)^(1/3): fck > 40 MPa.

Domínios de deformação do concreto

Então, a viga evolui do Estádio I (sem fissuras) até o Estádio III (ruptura) sob a ação de cargas, e, neste estado final, é necessário compreender os níveis de deformação do concreto armado.

Assim, esses níveis definem as faixas de deformação para dimensionar a seção transversal de concreto e as armaduras de uma viga no estado limite último, neste caso, entre os domínios 2 e 3.

Em resumo, estes são os limites dos domínios de dimensionamento das vigas, de acordo com a NBR 6118:2023.

• Domínio 2: (0 < ɛc < ɛcu, ɛs = ɛsu);
• Domínio 3: ɛc = ɛcu, ɛyd ≤ ɛs ≤ ɛsu;
• ɛc, ɛs : deformações no concreto e no aço;
• ɛcu: deformação de ruptura no concreto, que deve ser de até 0,35%;
• ɛsu: deformação de ruptura no aço (0,1%);

Por exemplo, dependendo da classe de aço utilizada, os valores de ɛyd, valor correspondente no ponto de escoamento do aço, traduzem-se pela seguinte expressão:

• ɛyd = fyd (tensão de cálculo no escoamento) / ४s.Es);
• ४s : coeficiente de minoração do aço, usualmente igual a 1,15;
• Es : módulo de elasticidade do aço, igual a 210 GPa;
• Aço CA-25: fyd = 250 MPa; ɛyd = 1,03 x 10⁻³;
• Aço CA-50: fyd = 500 MPa; ɛyd = 2,07 x 10⁻³;
• Aço CA-60: fyd = 600 MPa; ɛyd = 4,48 x 10⁻³;

Em termos práticos, um dos cenários é dimensionar a viga para a flexão simples de modo que a ruptura ocorra pelo escoamento do aço, mas sem a falha prematura do concreto comprimido.

Assim, a viga vai avisando, por meio de fissuras visíveis e crescentes, “estou perto do meu limite”, dando margens para intervenções de segurança.

Prevenção de frágil ruptura em vigas de concreto

Dito isso, vale lembrar que evitar um colapso súbito na viga exige atenção aos limites da razão x/d, onde x é a linha neutra e d a altura útil.

Logo, para que a viga tenha margem de segurança, evitando rupturas bruscas e repentinas, a norma brasileira estabelece os seguintes limites:

• x/d ≤ 0,45 para fck ≤ 50 MPa.
• x/d ≤ 0,35 para concretos mais resistentes: 50 MPa < fck ≤ 90 MPa.

Assim, sem essa regra, seria possível dimensionar vigas “superarmadas”, nas quais o concreto atinge a ruptura antes do aço escoar, devido ao excesso de armadura, caracterizando-se uma ruptura frágil.

Porém, se for necessário manter a altura da viga, seja por limitações arquitetônicas ou de projeto, e o cálculo indicar uma quantidade excessiva de aço, o que fazer?

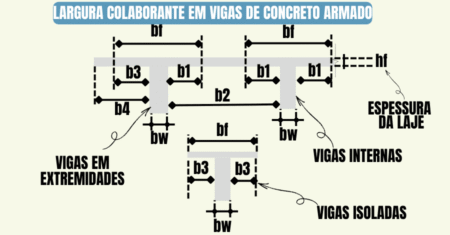
Portanto, uma solução prática é adotar uma armadura dupla, ou seja, colocar barras adicionais também na zona comprimida da seção, ou então adotar uma seção em forma de T.

Equações de dimensionamento para flexão simples

A propósito, conforme já explicado, a norma NBR 6118 permite substituir o diagrama real de tensões de compressão do concreto por uma forma retangular equivalente constante.

Assim, o grande benefício desta simplificação é que as equações de equilíbrio são semelhantes em todos os domínios de deformação.

Logo, é mais fácil de determinar a resultante de compressão, pois as diferenças entre as equações gerais e simplificadas são desprezíveis, embora sejam mais acentuadas no domínio 2.

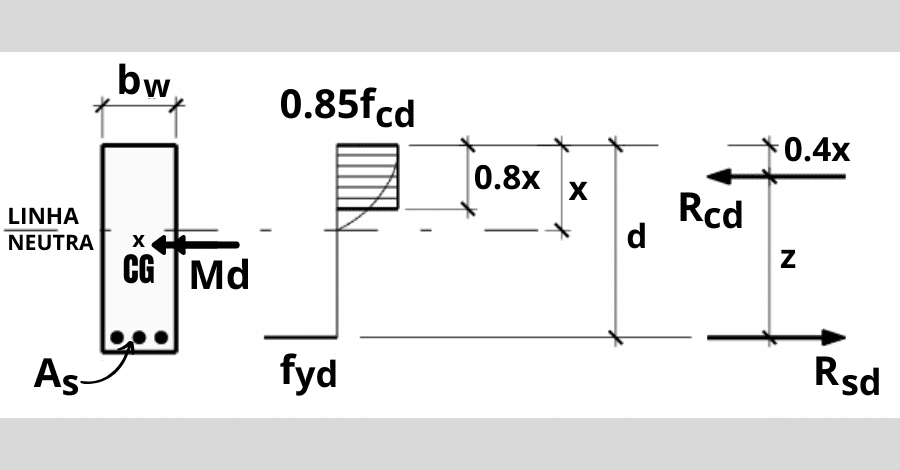
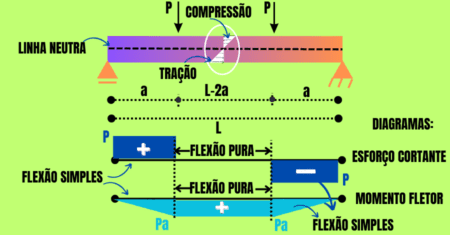
Para garantir o equilíbrio entre o momento fletor de cálculo (Md) e as forças solicitantes de tração na armadura (Rsd) e compressão do concreto (Rcd), ver a figura acima, tem-se:

• Rcd = Rsd; (1)
• Md=Rcd . z; (2)
• Md=Rsd . z; (3)
• Rcd=0.85.fcd.bw.0,8.x; (4)
• Rs = As.fyd; (5)
• z = d – 0,4.x; (6)

Portanto, substituem-se as equações (5) e (6) em (2) e (3), respectivamente:

• Md = As . fyd . (d – 0,4.x); (7)
• Md=0,68 . fcd . bw . x . (d-0,4.x) ; (8)

Manipulando as equações (7) e (8), obtém-se uma expressão para calcular o valor da linha neutra (x).

• x = 1,25 . d [ 1 ± (1- Md / (0,425.bw.d².fcd)^1/2]; (9)
• d = h – ∅_est – ∅_L/2 – cob; (10)

Onde:

• h, altura total e “d”, altura útil da viga;
• cob – cobrimento do concreto;
• ∅_est – diâmetro do estribo;
• ∅_L – diâmetro das barras de aço longitudinais;

Portanto, com os valores calculados, determina-se a armadura para a viga invertendo a equação (7):
As = Md / (fyd · (d – 0,4x)); (11)

Exemplo: flexão simples em vigas de concreto Armado

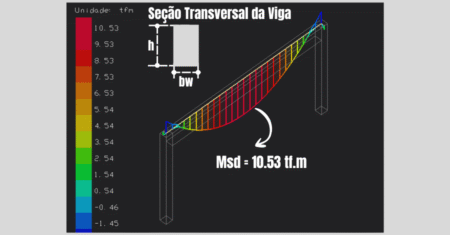
Então, a partir de uma estrutura hipotética definida usando o software TQS, (ver figura abaixo), calcule a armadura de flexão simples para as vigas iguais V3 e V4, com os seguintes dados:

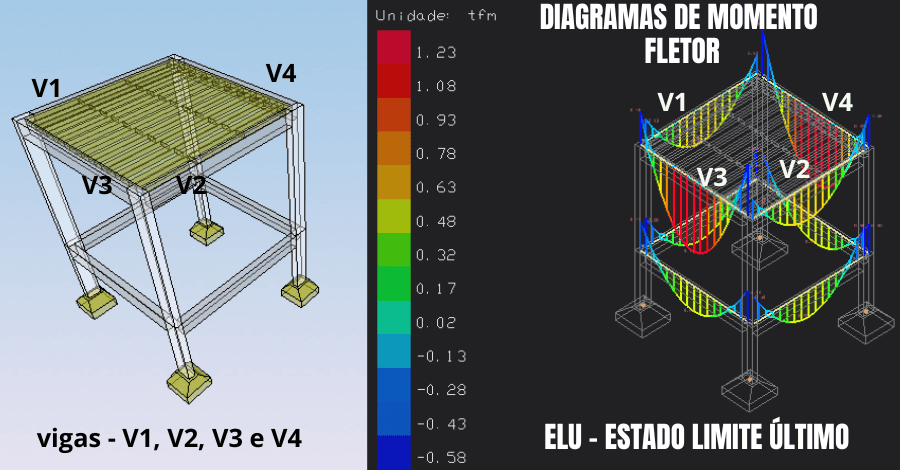
• fck = 20 MPa;
• fyd = 500 MPa;
• cob = 2,5 cm;
• ४s = 1,15;
• ४c =1,4;
• bw = 14 cm;
• Md = ४s . Mk = 1,4 . 1,23 = 1,72 tf.m = 172.200 kgf.cm;
• L = 316,5 cm;

Em contrapartida, estimam-se os valores iniciais para a altura da viga (h), diâmetros do estribo (∅_est) e da armadura (∅_L), altura útil “d”, e posteriormente, realizam os ajustes, caso sejam necessários:

• Pré-dimensionamento: h = L/10 = 316,5/10 = 31,65 cm. Adotar h= 30 cm;
• ∅_est = 5 mm.
• ∅_L = 10 mm;
• d = 30 – 2,5 – 1/2 – 0,5 = 26,5 cm;

Logo, vamos substituir os valores dos dados de entrada e usar a equação (9) para determinar a altura da linha neutra (x).

• x = 1,25 . 26,5 [ 1 ± (1- 172200/(0,425 . 14 , (26,5)².200/1,4)^1/2];
• Raízes da Equação: x₁ = 5,18 cm e x₂ = 61,07 cm; Adotar x=5,18 cm.

Verificações e Cálculo de Armaduras

Dito isso, verificar se a linha neutra está entre os limites dos domínios 2 e 3 e respeita o fator (x/d) máximo da norma brasileira.

• Limites do domínio 2: 0 ≤ x/d ≤ 0,26 (aço CA-50);
• Limites do domínio 3: 0,26 ≤ x/d ≤ 0,45; (fck ≤ 50 MPa);
• x/d (calculado) = 5,2/26,5 ≈ 0,195; (OK)

Caso seja necessário, adote um valor maior para h e refaça os cálculos até atingir os limites exigidos pela NBR-6118.

Feitos os devidos ajustes, o próximo passo é calcular a armadura para flexão simples usando a equação (11).

• As = 172200 / ((5000/1,15) × (26,5 – 0,4 × 5,2));
• As = 1,62 cm²;

Portanto, conforme figura abaixo, os valores da linha neutra (x) e da armadura de aço (As) calculados, estão em conformidade com a calculadora do TQS, ver figura abaixo.

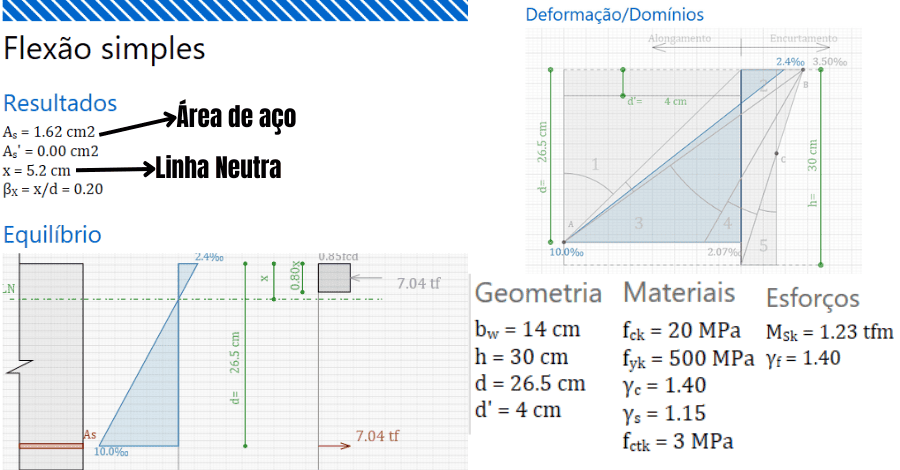
Em contrapartida, verificam-se os limites de armadura mínima (Asmin) e máxima (Asmax) de acordo com a NBR-6118 para fck=20 MPa.

• Asmin = 0,15%. bw . h = 0,0015 . 14 . 30 = 0,63 cm² < As
• Asmax = 4% bw.h = 0,04 . 14 . 30 = 16,8 cm² > As

Portanto, o propósito deste exemplo foi demonstrar de modo simples e prático o cálculo da armadura longitudinal de vigas de concreto no ELU.

Dito isso, para valores de fck superiores a 50 MPa ajustam-se os valores dos parâmetros ∝c e ηc de acordo com a norma, seguindo o mesmo roteiro de cálculo.

Considerações finais.

Então, o mecanismo de flexão simples em vigas de concreto armado foi avaliado considerando as simplificações adotadas pela norma brasileira NBR 6118.

Assim, o engenheiro precisa entender e fazer essas contas manualmente; portanto, o software torna-se um aliado importante para agilizar e acelerar o desenvolvimento dos projetos.

Porém, outras verificações são necessárias, como o estado limite de serviço e o cálculo de armaduras complementares, incluindo os estribos.

Aliás, para aprimorar a leitura e o entendimento do assunto, leia os artigos abaixo:

• Estádios do concreto armado.
• Domínios de deformação do concreto armado.