Flambagem de Pilares Sob Uma Ótica Bem Diferente

Muitos temas da engenharia estrutural continuam sendo fonte recorrente de dúvidas, más interpretações e a flambagem de pilares é um exemplo clássico.

Entre o pilar perfeito, retilíneo e com vínculos bem definidos, como descrito na teoria, e o pilar real, moldado em obra e inserido num sistema estrutural, existe um espaço ocupado pelo conhecimento prático do engenheiro.

Nesse contexto, diversas escolhas de projeto, frequentemente conservadoras, surgem menos da teoria idealizada e mais da experiência adquirida ao longo da prática profissional.

Este artigo não tem o objetivo de deduzir equações consagradas sobre a flambagem de pilares, amplamente discutidas no meio acadêmico e técnico.

A proposta é abordar o fenômeno a partir de seus parâmetros fundamentais, comuns aos pilares de diferentes materiais, com destaque para a interpretação desses conceitos no projeto estrutural.

Se esse tema te interessa sob uma visão mais prática e reflexiva, fica o convite à leitura, compartilhamento e também à contribuição com seu próprio ponto de vista.

Aspectos iniciais sobre a flambagem de pilares

Então, a flambagem de pilares refere-se ao encurvamento lateral, gradual ou repentino, quando submetidos a determinada intensidade de carga axial de compressão e/ou momento fletor.

A sua ocorrência é independente da resistência do material à compressão; aliás, trata-se de uma perda de estabilidade estrutural do pilar.

Assim, ele desvia de sua configuração geométrica inicial de equilíbrio e passa a se deformar lateralmente.

Por esse motivo, a flambagem associa-se a um fenômeno de flexão do pilar, podendo ocorrer mesmo que as tensões ainda se encontrem no regime elástico do material.

Esse processo provoca uma redução significativa da rigidez do pilar, compromete sua capacidade resistente e pode levar a um colapso estrutural.

O elo de ligação entre teoria e prática

No ambiente da obra, nenhum pilar é perfeitamente retilíneo, nenhum carregamento é aplicado rigorosamente no seu centro e nenhum vínculo se comporta exatamente como o modelo é idealizado na teoria.

Por exemplo, surgem imperfeições geométricas e excentricidades nas cargas, que exercem grande influência na resposta dos pilares submetidos à compressão.

Sobretudo, muita atenção à interação dos pilares com outros elementos estruturais, tais como vigas, lajes e situações em que o topo do pilar se encontra livre.

Tudo isso pode modificar de forma significativa as condições de vinculação do pilar e, por consequência, o seu comportamento estrutural frente à instabilidade e à resistência à flambagem.

Assim, a definição das condições de apoio nas extremidades dos pilares, quando coerente com o funcionamento real do sistema estrutural, tende a afastar-se das hipóteses da teoria clássica.

Nesse contexto, o papel do engenheiro estrutural torna-se decisivo, pois a sua experiência e sensibilidade técnica permitem interpretar corretamente o grau de restrição oferecido pelos elementos adjacentes aos pilares.

Além de traduzir essa leitura em escolhas de projeto, pois elas conduzem a um dimensionamento de pilares com soluções mais conservadoras ou mais arrojadas. Porém, sempre dentro de um equilíbrio entre:

• Segurança;
• Coerência estrutural;
• Racionalidade construtiva;

Em resumo, a sensibilidade de um pilar à flambagem é determinada pela interação entre alguns parâmetros fundamentais, dentre os quais se destacam:

• Comprimento do pilar;
• Condições de apoio;
• Índice de esbeltez;

Nos próximos tópicos, esses parâmetros serão discutidos de forma mais integrada, com foco na sua interpretação prática no projeto estrutural.

Parâmetros que influenciam a flambagem de pilares

Para começar, o comprimento de flambagem representa a distância entre pontos de inflexão da linha deformada do pilar, isto é, regiões onde o momento fletor é nulo.

Conforme definido na teoria clássica em resistência dos materiais, o comprimento de flambagem (Lf) de um pilar ou barra comprimida é expresso como:

• Lf = K x L (1)

Onde L é o comprimento geométrico do pilar e K é o coeficiente de flambagem, associado às condições de vinculação em suas extremidades, conforme ilustrado na Figura 1:

• 1 – Rótulas: K = 1.
• 2 – Engaste e extremidade livre: K = 2.
• 3 – Engastes: K = 0.5;
• 4 – Engaste e um apoio simples: K = 0.7;

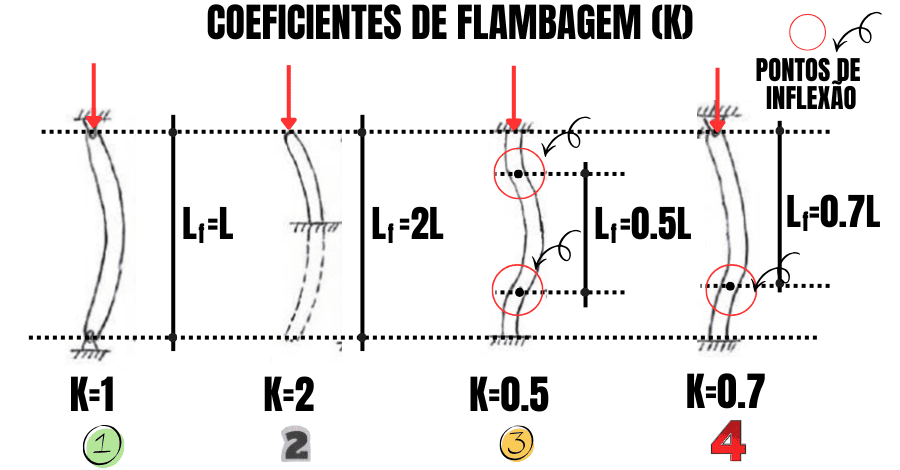
Estes valores correspondem a casos teóricos clássicos, definidos a partir de vínculos ideais, como engastes perfeitos, apoios sem rigidez à rotação ou extremidade livre.

Pontos de atenção em situações de projeto

Na prática, pilares em balanço, ou mesmo com vigas conectadas a eles, também em balanço, caracterizam uma situação de um pilar com extremidade livre.

Por outro lado, a presença de vigas, sejam biapoiadas ou contínuas, bem como de lajes, pode restringir os deslocamentos laterais e/ou as rotações do pilar ao qual estão conectadas.

A laje treliçada merece atenção especial, pois pode apresentar restrição ineficiente ao movimento lateral de um pilar ligado a ela, na direção perpendicular às nervuras.

Essas restrições não dependem só do material do pilar, seja concreto, aço ou madeira, mas também da rigidez relativa entre os elementos estruturais conectados.

Assim, um mesmo pilar pode apresentar comprimentos de flambagem distintos em direções ortogonais, refletindo diferentes níveis de restrição ao deslocamento lateral.

Por outro lado, alguns softwares comerciais calculam o coeficiente de flambagem a partir da concepção estrutural definida pelo engenheiro.

No entanto, cabe ao projetista avaliar fielmente se o comportamento assumido pelo programa é coerente com a realidade estrutural e, caso necessário, realizar ajustes no modelo estrutural.

Esses ajustes assumem um caráter mais conservador quando se admite menor restrição aos deslocamentos ou rotações do pilar.

Deste modo, resulta em comprimentos de flambagem maiores, conduzindo a verificações mais rigorosas e a favor da segurança.

Portanto, com o comprimento de flambagem definido, torna-se possível introduzir um outro parâmetro fundamental na análise da flambagem de pilares: o Índice de esbeltez.

Índice de esbeltez de pilares

Bem, o índice de esbeltez dos pilares é geralmente representado pela letra λ, definido pela relação entre o comprimento de flambagem (Lf) e o raio de giração do pilar (r):

• λ= Lf / r; (2)

Assim, o raio de giração segue a formulação clássica, isto é, igual à raiz quadrada da relação entre o momento de inércia da seção do pilar (I) e a área de sua seção transversal (A):

• r = (I/A)^1/2 (3)

Definem-se os eixos principais da seção transversal, passando pelo seu centroide, e indicam as direções em que o pilar apresenta menor ou maior propensão à flambagem, conforme o valor do índice de esbeltez. Assim, verifica-se o índice de esbeltez nas direções x e y, resultando em dois valores, Figura 2:

• λx = Lfx / rx; (4)
• λy= Lfy / ry; (5)

Deste modo, esses valores são comparados com índices limites estabelecidos nas normas brasileiras, os quais variam conforme o tipo de material estrutural:

• NBR 6118: concreto armado.
• NBR 8800: aço.
• NBR 7190: madeira.

Além disso, esses índices são organizados em faixas, permitindo classificar os pilares conforme seu grau de esbeltez.

Dito isso, a relação entre comprimento e seção transversal de um pilar indica quão robusto ou mais ele é sensível à flambagem.

Em termos gerais, à medida que o índice de esbeltez aumenta, passam a ser considerados efeitos adicionais no cálculo do pilar, como:

• Imperfeições geométricas,
• Efeitos de segunda ordem.
• Fluência.

Existe, ainda, um limite superior a partir do qual o pilar deixa de atender às hipóteses usuais de projeto, caracterizando uma condição inadequada sob o ponto de vista estrutural.

Exemplo de cálculo do índice de esbeltez de um pilar

Considere, de forma hipotética, um pilar com seção transversal retangular de dimensões (b=14 cm; h=30 cm) e comprimento de flambagem Lf = 3 m, considerado o pilar travado por vigas nas direções x e y (K=1), ver Figura 2;

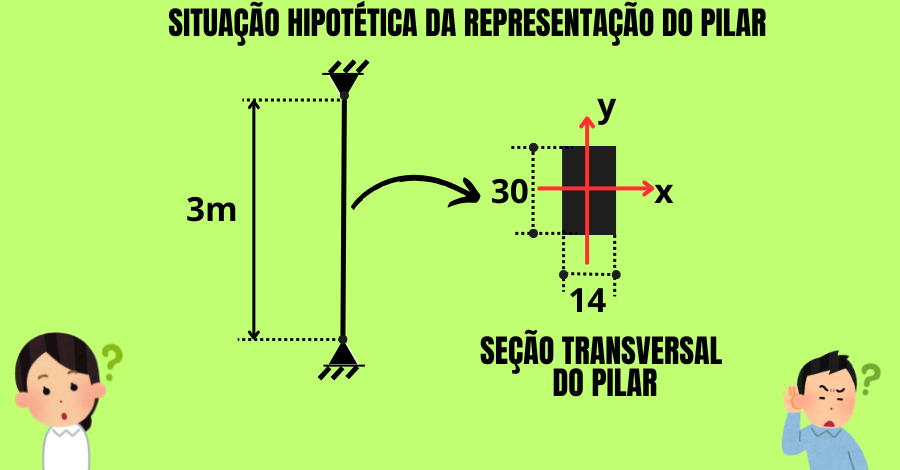
O cálculo dos momentos de inércia segue as fórmulas padrão de resistência dos materiais, de acordo com a geometria e direções da seção do pilar; neste caso, uma seção retangular.

Assim, obtêm-se a área da seção do pilar (A), raios de giração (rx e ry) e os momentos de inércia (Ix e Iy) nas direções x e y:

• A = 14 x 30 = 420 cm²;
• Ix = b x h³ / 12 = 14 x 30³ / 12 ; Ix = 31500 cm⁴;
• Iy = h x b³ / 12 = 30 x 14³ / 12 ; Iy = 6860 cm⁴;
• rx = (Ix/A)½ = (31500/420)^1/2 ; rx=8.66 cm;
• ry = (Iy/A)½ = (6860/420)^1/2 ; ry=4.04 cm;

Logo, pelas equações (4) e (5), obtêm-se os índices de esbeltez em ambas as direções do pilar:

• λx = Lfx / rx = 300 / 8.66 ; λx = 34.64;
• λy = Lfy / ry = 300 / 4.04 ; λy = 74.25;

Embora o momento de inércia da seção seja maior em torno do eixo x, isso não representa uma condição mais crítica para a flambagem. Pelo contrário, a maior rigidez desse eixo reduz a sensibilidade do pilar a deslocamentos laterais.

Assim, a direção mais desfavorável à flambagem é aquela associada ao menor momento de inércia; neste caso, o eixo y, devido a menor dimensão da seção transversal do pilar nesta direção.

Nessa direção, o raio de giração é menor; logo, resulta em um índice de esbeltez mais elevado e maior propensão ao encurvamento lateral do pilar.

Considerações finais sobre Flambagem de Pilares

A análise da flambagem de pilares evidencia ser mais do que um problema puramente matemático, pois trata-se de uma questão de concepção e interpretação estrutural.

Nesse contexto, o coeficiente de flambagem e o comprimento efetivo não devem ser encarados apenas como parâmetros tabelados, mas como representações simplificadas de decisões de projeto.

Compreender o seu significado físico torna-se tão importante quanto aplicá-los corretamente nos projetos estruturais.

Portanto, cabe ao engenheiro avaliar com senso crítico os resultados obtidos, seja por cálculos manuais, uso de planilhas ou softwares de cálculo, reconhecendo os seus limites e hipóteses.