Laje Maciça Unidirecional Isolada: Cálculo Manual dos Esforços Solicitantes

Um dos elementos estruturais mais tradicionais dos primórdios da engenharia civil é a laje maciça unidirecional isolada.

Aliás, compreender o mecanismo básico de funcionamento das lajes é uma etapa indispensável para o engenheiro interpretar fielmente análises estruturais mais avançadas e os resultados fornecidos por softwares comerciais.

Por outro lado, com a ampla disseminação dos métodos numéricos e das ferramentas computacionais, os projetos estruturais ganharam velocidade e precisão.

Assim, esse avanço também afastou muitos profissionais da compreensão física dos modelos adotados, tornando a análise estrutural, em certos casos, um processo bastante operacional.

Dito isso, aprenderemos um método clássico de cálculo manual dos esforços de uma laje maciça unidirecional isolada.

Deste modo, você determina diretamente os momentos fletores e as reações de apoio da laje, pois fornece uma base conceitual bastante sólida para análises mais sofisticadas.

O que é uma laje maciça unidirecional isolada?

Então, ela é uma laje de concreto armado moldada in loco, cuja resistência aos momentos fletores se desenvolve com predominância em uma única direção.

A propósito, o termo “isolada” indica a ausência de continuidade com lajes adjacentes ou vizinhas em suas extremidades.

Assim, a laje encontra-se delimitada por vigas em todas as suas bordas e analisa-se de forma independente (Figura 1).

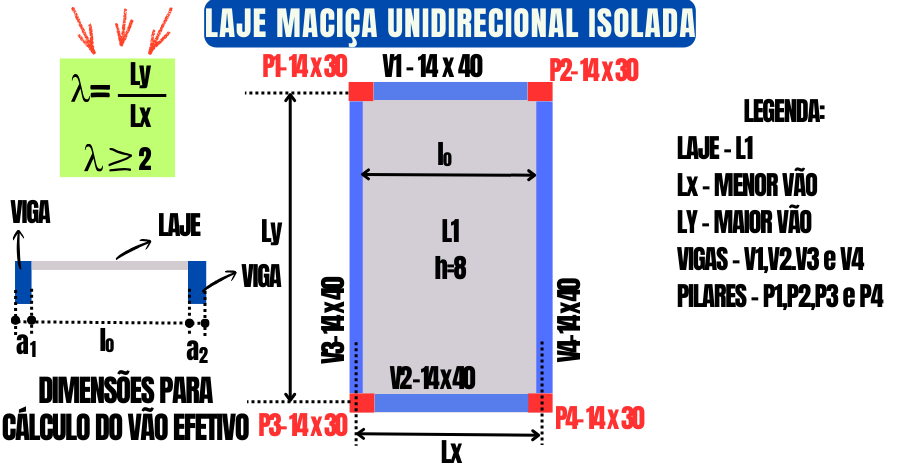
Detrmina-se a geometria da laje por meio do projeto de arquitetura e das exigências funcionais do ambiente, tais como:

• Dimensões em planta (Lx e Ly);
• Posição das vigas de contorno;

Nessa configuração, Lx representa o menor vão, e Ly, o maior vão da laje.

A armadura principal é disposta na direção do menor vão, onde se concentram os maiores momentos fletores da laje, situação similar à laje treliçada.

Por outro lado, na direção transversal (Ly), adota-se apenas uma armadura de distribuição, cuja função principal é:

• Controlar a fissuração;
• Absorver efeitos de retração e variações térmicas;
• Garantir a integridade e o travamento da armadura principal;

Inclusive, a presença da armadura transversal não altera o caráter unidirecional da laje, pois sua contribuição resistente aos momentos fletores nas direções principais da laje é nula.

Pré-dimensionamento da espessura da laje

Para começar, define-se a espessura da laje na etapa de pré-dimensionamento, considerando critérios de resistência, rigidez e controle de deformações.

Como referência inicial, podem ser adotados os valores de altura da laje (h) mínimos recomendados pela NBR 6118:

• h = 7 cm: laje de cobertura;
• h = 8 cm: laje de piso;
• h = 10 cm: lajes para circulação de veículos com peso máximo de 3 toneladas;
• h = 12 cm: lajes com circulação de veículos com peso superior a 3 toneladas;

Assim, ajusta-se posteriormente a espessura da laje em função dos esforços solicitantes e da verificação das flechas em estado limite de serviço.

Dito isso, parte-se para o cálculo dos vãos efetivos da laje (lef), definidos conforme os critérios da norma NBR-6118.

Logo, considera-se a distância livre entre os apoios para cada direção da laje (lo), a largura das vigas de contorno (a1 ou a2) e a espessura da laje (h); ver Figura 1:

• lef = lo + a1 + a2;
• a1 ≤ menor valor (a1/2 e 0,3h);
• a2 ≤ menor valor (a2/2 e 0,3h);

Vinculação das bordas da laje

De forma simplificada, consideram-se as bordas da laje apoiadas sobre as vigas de contorno, admitindo-se apoios simples em ambas as direções.

Entretanto, uma análise mais refinada pode exigir a consideração de engastes parciais ou totais, em função da rigidez das vigas de bordo e da capacidade delas de resistir aos esforços de torção.

Desta forma, a definição das condições de apoio depende do critério adotado pelo engenheiro estrutural e influencia diretamente os valores dos momentos fletores obtidos no cálculo.

Composição das cargas na laje

Em geral, a distribuição de cargas em lajes engloba as seguintes parcelas:

• Peso próprio;
• Cargas permanentes;
• Sobrecargas;

A princípio, obtém-se o peso próprio da laje (go) pela multiplicação do peso específico do concreto armado (૪c) pela espessura estimada da laje (h):
go = ૪c x h;

De forma usual, adota-se o valor de (૪c = 2.5 tf/m³ ), conforme a NBR-6120;

Por outro lado, as cargas permanentes (gper) caracterizam-se pela presença de pisos e contrapisos sobre a laje, podendo ser estimadas de maneira análoga ao peso próprio:

• gp = ૪p x tp;
• gcp = ૪cp × tcp;
• gper = gp + gcp;

Onde ૪p e ૪cp representam os pesos específicos do piso e contrapiso, valores obtidos na NBR-6120 ou em catálogos comerciais, e tp e tcp, suas respectivas espessuras.

Pontos de atenção: Paredes em laje maciça unidirecional isolada.

Ainda mais, como parcela adicional, na presença de paredes, estima-se o peso de parede por unidade de área por meio da expressão:

• ૪par = ૪alv x talv + ૪rev x trev;

Onde ૪par corresponde ao peso específico da parede, com ૪alv e ૪rev representando os pesos específicos da alvenaria e do revestimento, talv e trev suas respectivas espessuras.

Mais uma vez, os pesos específicos dos materiais são obtidos pela norma brasileira NBR-6120 ou pelos catálogos de fabricantes.

Em situações nas quais a laje contém ambientes com paredes dispostas em diversas direções, utiliza-se uma aproximação global para a carga média por metro quadrado de paredes na laje:

• gpar = (૪par.hpar.lp) / Alaje;

Sendo hpar a altura da parede, lp o perímetro total das paredes e Alaje a área da laje, considerando retangular (Lx.Ly).

Em seguida, de forma simplificada, analisa-se a ação das paredes sobre lajes maciças unidirecionais isoladas em dois casos típicos (Figura 2):

• Caso 1: parede paralela à direção principal da laje (Lx);
• Caso 2: Parede perpendicular à direção principal da laje (Lx);

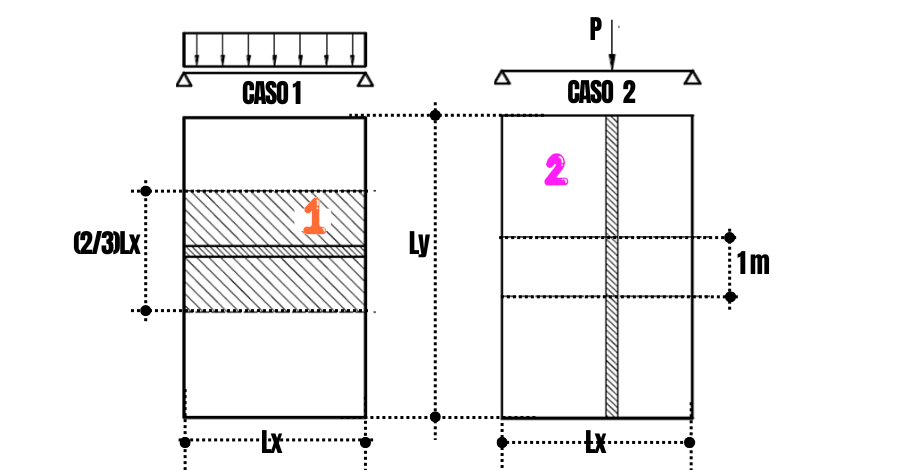
No Caso 1, estima-se a carga da parede (gpar) distribuída em uma área de influência da laje, admitida de forma aproximada, com largura Lx e comprimento (2/3) Lx:

• Pp = ૪par × hpar × lp;
• gpar = Pp / [(2/3 Lx) . Lx];

Onde lp representa o comprimento da parede na direção x.

Bem como, no caso 2, a carga da parede é idealizada como uma força concentrada (P) que representa o efeito da parede sobre a laje:

• P = ૪par x hpar x 1 m;

Cargas Variáveis

Além das ações permanentes, a NBR 6120 considera a ação de sobrecargas (qs) nas lajes, representadas por cargas variáveis associadas ao uso da edificação.

Assim, definem-se esses valores com base na categoria de ocupação do ambiente analisado. Como referência, podem ser citados alguns exemplos usuais:

• Dormitórios, sala e cozinha em edifícios residenciais: qs = 1.5 kN/m²;
• Salas de leitura em bibliotecas: com estantes (qs = 4 kN/m²); sem estantes (qs = 3 kN/m²).
• Plateias de cinema com assentos fixos: qs = 4 kN/m²;

Sobretudo, os valores apresentados correspondem apenas a situações típicas, devendo a escolha da sobrecarga ser compatível com o uso específico do ambiente considerado.

Em resumo, obtém-se a carga total atuante na laje (qt) pela soma das parcelas consideradas acima:

• qt = go + gper + gpar + qs;

Aliás, para uma abordagem mais detalhada sobre carregamentos em estruturas de concreto armado, recomenda-se a leitura do artigo:
Ações nas estruturas de concreto armado

Hipóteses básicas do modelo de cálculo

Em primeiro lugar, o modelo tradicional de cálculo da laje maciça unidirecional isolada baseia-se nas seguintes hipóteses simplificadoras:

• A laje é analisada como um conjunto de faixas independentes, paralelas à direção principal da armadura (direção Lx);
• Cada faixa comporta-se como uma viga de largura unitária (1,00 m), apoiada nas vigas de contorno;
• As cargas atuam de forma distribuída e uniforme ao longo das faixas da laje;

Além disso, a condição geométrica (Ly / Lx ≥ 2) caracteriza o comportamento unidirecional da laje.

Portanto, essas hipóteses permitem a utilização de modelos analíticos claros e eficazes, adequados à compreensão do comportamento estrutural da laje e à determinação dos esforços solicitantes principais.

Esforços solicitantes na laje maciça unidirecional isolada

Então, com base no modelo simplificado já descrito, determinam-se os esforços solicitantes considerando cada faixa da laje como uma viga de largura unitária (1,00 m) disposta na direção Lx.

Assim, o carregamento atuante em cada faixa é representado por uma carga distribuída equivalente, linear dada por:

• q = qt × 1,00 m;

Onde qt corresponde à carga total por unidade de área atuante na laje.

Logo, as faixas da laje podem ser analisadas considerando diferentes condições de vinculação nas extremidades, dependendo da rigidez das vigas de contorno (Figura 3):

• Caso A: Faixa simplesmente apoiada, adequada quando as vigas de bordo apresentam baixa rigidez à rotação.
• Caso B: engaste parcial representa uma condição intermediária entre os casos A e C.
• Caso C: faixa bi-engastada, aplicável quando as vigas de contorno possuem elevada rigidez à flexão e à torção.

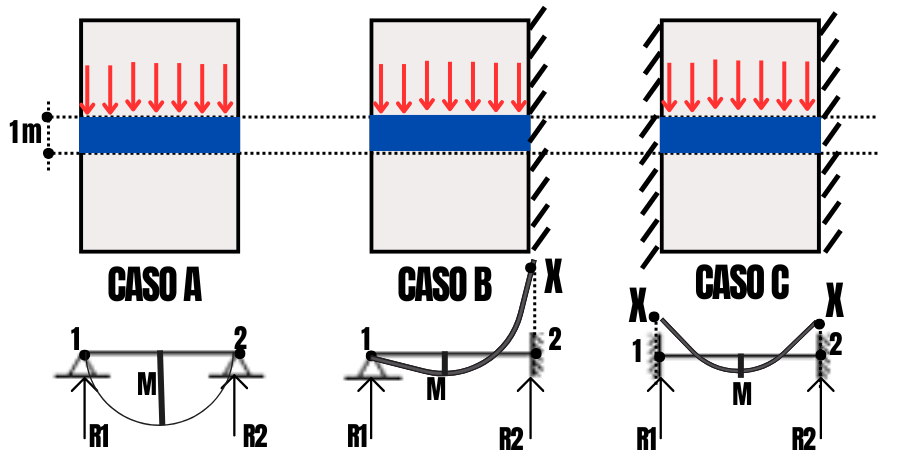
Em todos os casos, as reações de apoio por unidade de comprimento decorrem da ação de uma carga distribuída e uniforme ao longo da faixa da laje, sendo transmitidas às vigas periféricas.

Assim, os esforços solicitantes, por metro linear, podem ser estimados da seguinte forma:

Faixa simplesmente apoiada

• Reações: R1 = R2 = (q · Lx) / 2;
• Momento positivo: M = (q · Lx²) / 8;

Faixa bi-engastada

• Reações: R1 = R2 = q·Lx / 2;
• Momento positivo: M = q·Lx² / 24;
• Momento negativo: X = − q·Lx² / 12;

Engaste parcial

• Reações: R1 = 3q·Lx / 8;  R2 = 5q·Lx / 8;
• Momento positivo: M = q·Lx² / 14.22;
• Momento negativo: X = – q·Lx² / 8;

Com o propósito, esses resultados fornecem estimativas diretas dos esforços solicitantes, servindo como referência para o dimensionamento das armaduras e para a validação de modelos numéricos mais sofisticados.

Exemplo de cálculo: laje maciça unidirecional isolada

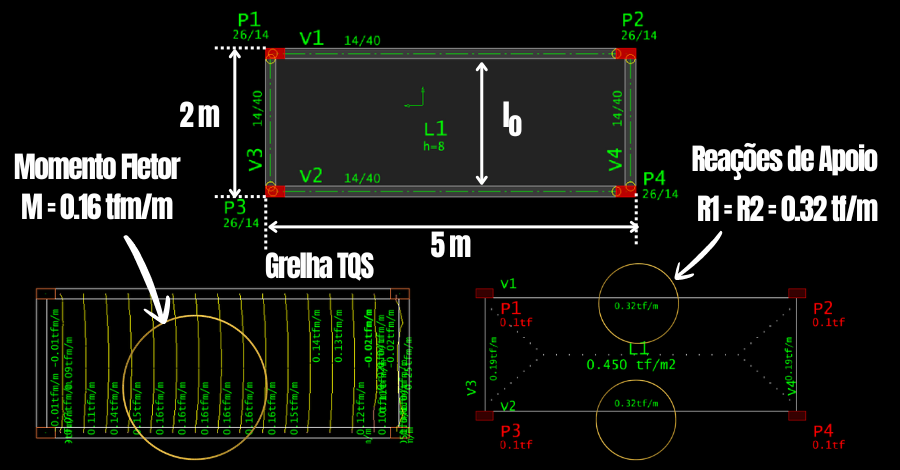
Por exemplo, considere uma laje maciça unidirecional isolada, apoiada em vigas nas quatro bordas (Figura 4), submetida a um carregamento uniforme característico e sem a presença de paredes. Adotam-se os seguintes dados:

• Vão livre entre apoios: Lox = 172 cm; Loy = 448 cm;
• Largura das vigas de contorno: bw = 14 cm;
• Espessura da laje: h = 8 cm;
• Peso específico do concreto armado: ૪c = 2.5 tf/m3;
• Peso próprio da laje: go = 2.5 x 0.08 = 0.2 tf/m²;
• Cargas permanentes adicionais (piso e revestimentos): gper = 0.1 tf/m²
• Sobrecarga de utilização: qs = 0.15 tf/m²;

Além disso, admite-se também a laje idealizada como simplesmente apoiada nas vigas laterais, pois estas têm baixa rigidez à torção com largura de apenas 14 cm.

Portanto, o objetivo é calcular os esforços solicitantes na laje com base no modelo clássico de faixas independentes para lajes unidirecionais, metodologia discutida neste artigo.

Cálculo dos esforços solicitantes na laje maciça unidirecional isolada

Em princípio, o primeiro passo é calcular a carga total característica atuante na laje por m², somando as parcelas atuantes:

• qt = go + gper + qs = 0.2 + 0.1 + 0.15 = 0.45 tf/m²;

Assim como a análise é feita por faixas de largura unitária (1,00 m), a carga distribuída linearmente torna-se simples:

• q = 0.45 tf/m² x 1 m = 0.45 tf/m;

Por conseguinte, o segundo passo é obter o vão efetivo da laje (lef), conforme os critérios da NBR 6118, considerando a distância livre entre apoios (lo) e a contribuição das larguras das vigas:

• a1 ≤ (a1/2 e 0.3h) = (14/2 e 0.3 × 8) = (7 e 2.4) = 2.4 cm;
• a2 ≤ (a2/2 e 0.3h) = (14/2 e 0.3×8) = (7 e 2.4) = 2.4 cm;
• lef = lo + a1 + a2 = 172 + 2.4 + 2.4 = 176.8 cm;

Deste modo, calculam-se os esforços característicos por unidade de metro linear na laje como uma viga biapoiada submetida a carga distribuída linear (q) e vão efetivo (lef):

• Reações: R1 = R2 = q·lef / 2 = (0.45 x 1.768)/2 = 0.3978 tf/m;
• Momento positivo: M = q·lef² / 8 = (0.45 x 1.768²)/8 = 0.176 tf.m/m;

Comparação do modelo com o software TQS

No entanto, como estimativa, obteve-se os resultados do mesmo modelo pelo software TQS (Figura 4):

• R1=R2 = 0.32 tf/m: Teoría das linhas de Ruptura;
• M≈0.16 tfm/m: Grelha TQS;

Conforme já visto acima, a análise manual, baseada na idealização da laje como uma viga biapoiada de largura unitária, conduz a um momento fletor positivo de 0.176 tf·m/m.

Porém, o modelo de grelha do TQS resulta em um momento fletor da ordem de 0.16 tf·m/m, valor 10% inferior, o que era esperado em função da redistribuição dos esforços promovida pela modelagem bidimensional do pavimento.

Por outro lado, quanto às reações de apoio, nota-se que o valor obtido pelo TQS, associado à teoria das linhas de ruptura, é cerca de 18% inferior ao valor calculado pela análise unidimensional.

Aliás, a teoria das linhas de ruptura distribui as cargas atuantes na laje entre as vigas de contorno nas duas direções, assim, transfere-se parte do carregamento para as vigas perpendiculares à faixa analisada.

Logo, a parcela da carga efetivamente absorvida por cada viga ao longo do vão considerado é reduzida.

Portanto, resulta em menores valores de reações de apoio quando comparados à análise unidimensional por faixas independentes.

Considerações finais

Em suma, embora os projetos estruturais atuais utilizem intensivamente softwares comerciais cada vez mais avançados, o cálculo manual continua sendo uma ferramenta essencial para o engenheiro estrutural.

Assim, o modelo simples de uma laje maciça unidirecional isolada permite estimar a ordem de grandeza dos esforços solicitantes e interpretar criticamente os resultados fornecidos por análises numéricas.

Bem como, base conceitual importante e prática para validação de estruturas com comportamento semelhante, como as lajes treliçadas e nervuradas unidirecionais.

Gostou do artigo? Aproveite o espaço dos comentários e deixe seu ponto de vista.