Tensão Verdadeira em Engenharia: Você Conhece?

A primeira vez que tive contato com a expressão ‘tensão verdadeira‘ foi durante uma disciplina de Teoria da Plasticidade, no doutorado.

Assim, até aquele momento, meu conhecimento se limitava às relações clássicas de tensão, também chamadas de tensão de engenharia ou nominal, nas quais se aprende ainda no ensino médio.

• Tensão = força / área (válida na região elástica do material);

Por exemplo, em aplicações mais refinadas de engenharia usando o método dos elementos finitos, os conceitos de tensão e deformação verdadeira são bastante relevantes, portanto, prossiga na leitura e compreenda tudo.

Tensão e deformação na engenharia

Realizam-se ensaios de tração com os materiais e assim, define-se a tensão (σ_eng) e a deformação de engenharia (ε_eng):

• σ_eng = F/A_o; força/área original (1)
• ε_eng = ΔL (variação de comprimento) / L_o (comprimento original); (2)

A propósito, o cálculo da tensão e da deformação de engenharia considera sempre a área e o comprimento iniciais do corpo de prova, Equações (1) e (2), sem levar em conta as alterações que ocorrem durante o ensaio.

Essas definições são simples, mas muito úteis na região elástica, onde a tensão e a deformação apresentam relação linear, e permitem determinar as propriedades elásticas do material.

• Módulo de elasticidade;
• Coeficiente de Poisson;
• Tensão de escoamento;

Por outro lado, tanto a área quanto o comprimento do corpo de prova se alteram ao longo dos testes experimentais, por isso, o cálculo das tensões e deformações verdadeiras leva em conta esse efeito.

Materiais dúcteis e frágeis

Então, o uso da curva tensão versus deformação verdadeira torna-se bastante relevante em materiais dúcteis, como os metais:

• Aço;
• Alumínio;
• Titânio;

Aliás, esses materiais apresentam grande capacidade de alongamento antes da ruptura, definindo duas regiões bem distintas no gráfico tensão x deformação: a parte elástica e a plástica, Figura 1.

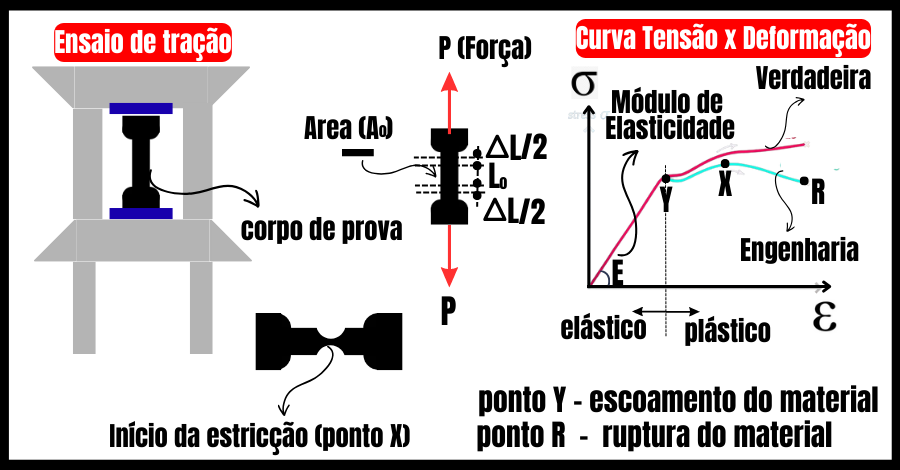
Em contrapartida, os materiais frágeis rompem de forma quase imediata ao atingir a tensão máxima, sem escoamento e sem uma região plástica bem definida, por exemplo:

• Compósitos;
• Concreto;
• Vidro;

Porém, em muitos projetos de engenharia, a análise estrutural ocorre dentro do regime elástico, no qual as curvas tensão-deformação de engenharia apresentam valores muito próximos da verdadeira.

No entanto, existem casos em que necessita-se de uma análise mais profunda do material na região plástica até a ruptura, e vale a utilização da curva tensão versus deformação verdadeira.

Os softwares de elementos finitos, como o Abaqus e o Ansys, permitem uma avaliação mais precisa do material na região plástica.

Portanto, para cada situação, vale o julgamento do engenheiro, com sua experiência e conhecimentos, para tomar a decisão mais correta e necessária.

O que é tensão verdadeira?

Para obtê-la, parte-se dos valores de tensão e deformação de engenharia; por isso, foi necessário percorrer esses conceitos iniciais antes de avançar para a tensão verdadeira, em dois passos.

No primeiro passo, assume-se o volume do material constante durante os testes experimentais, ou seja, sem adicionar ou remover material.

Assim, ao multiplicar a área da seção transversal inicial (A_o) pelo comprimento inicial do corpo de prova (L_o), obtém-se um volume invariável durante os ensaios.

• A_o . L_o = Ai . Li ; Ai = (A_o · L_o) / Li; (3)
• A_o e L_o referem-se à área da seção transversal e comprimento inicial do corpo de prova;
• Ai e Li; área e volume em um tempo qualquer do ensaio;

No entanto, essa hipótese permanece válida até o início da estricção do corpo de prova, neste caso, o material sofre redução de área e de volume, ver Figura 1, ponto X.

Segundo Passo para Calcular a Tensão Verdadeira

Nesta etapa, define-se a tensão verdadeira (σ_verd) como a relação entre a força (Fi) e a área (Ai). e substitui-se (Ai) pela equação (3), válida para um instante qualquer i:

• σ_verd = Fi/Ai = (Fi · Li) / (A_o · L_o) ; (4)

Em seguida, manipula-se a equação (2) da deformação de engenharia (ε_eng), em função dos comprimentos Li e L_o , também no instante i:

• ε_eng = ΔL / Lo = (Li – L_o) / L_o = Li / L_o – 1; (5a)
• Li / L_o = ε_eng + 1; (5b)

Assim, substituem-se as equações (1) e (5b) na equação (4) e encontra-se a definição da tensão verdadeira (σ_verd):

• σ_verd = σ_eng · (ε_eng + 1); (6)

Logo, de posse da tensão e deformação de engenharia pelos ensaios de tração, obtém-se facilmente a tensão verdadeira pela equação (6).

Como obter a deformação verdadeira?

Para começar, vamos atualizar a definição de deformação, que é dada pela variação de comprimento dividida pelo comprimento total, para cada instante i de um ensaio.

• ε = ΔLi / Li; (7)

Em vez de relacionar a deformação com o comprimento inicial (L_o), considera-se o comprimento à medida que o ensaio se desenvolve para cada passo de carga.

Assim, define-se a deformação verdadeira pela soma das deformações em cada incremento do ensaio, formando um somatório, conforme ilustrado na Figura 2.

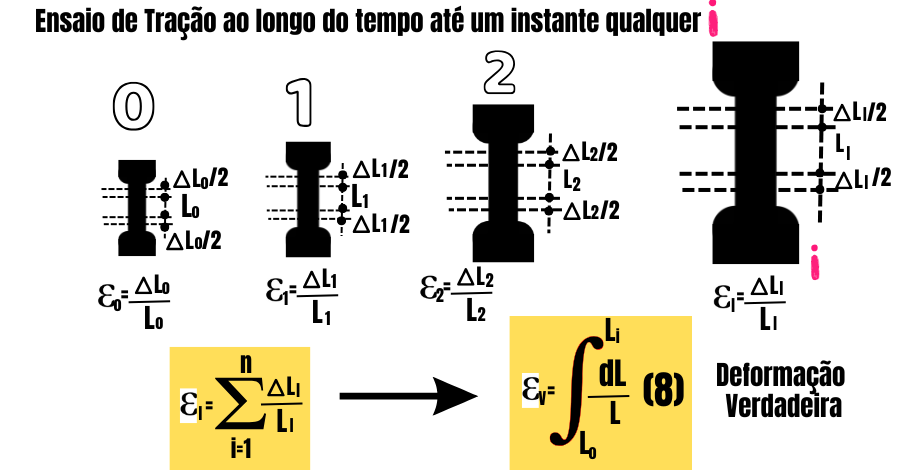
Do ponto de vista matemático, o somatório torna-se uma integral entre o comprimento inicial (L_o) e o final (Li), conforme a equação (8) na Figura 2.

Dito isso, com essas aproximações, evita-se fazer as medições de área e comprimento durante o decorrer do ensaio experimental, pois são tarefas bastante complicadas. Assim, a solução da equação (8) é o logaritmo natural:

• ε_verd = ln (Li / L_o); (9)

Portanto, chega-se à equação tradicional da deformação verdadeira, substitui Li/L_o já definido na equação (5b):

ε_verd = ln( ε_eng + 1); (10)

Aplicações práticas da tensão verdadeira

Primeiro de tudo, nas indústrias metalúrgicas, usar a tensão e deformação verdadeira ajuda a tornar os processos de conformação mais precisos e eficientes.

Esses conceitos são fundamentais em diversos processos nas empresas, como a laminação, extrusão, estampagem e forjamento, nos quais o material é submetido a grandes deformações plásticas.

Assim, os engenheiros conseguem ter mais precisão nos limites de resistência do material, ajustam as forças de operação, controlam a espessura final e até reduzem o risco de trincas.

Portanto, propicia uma geometria mais precisa e qualidade estrutural do produto final, contribuindo, assim, para a redução do desperdício de matéria-prima.

Por outro lado, os dados de tensão e deformação verdadeira são amplamente utilizados em simulações computacionais, em conjunto com o método dos elementos finitos.

Assim, os engenheiros se inspiram em soluções estruturais mais arrojadas e eficientes, pois aproveitam essa reserva de material, além do limite elástico.

Porém, de modo bem controlado e sempre em conformidade com os limites físicos do material e aspectos normativos.

Além disso, os pesquisadores aprofundam seu conhecimento sobre os materiais, propõem mais soluções estruturais e confrontam com os resultados experimentais.

Confira na figura abaixo comparando os gráficos das curvas tensão-deformação verdadeira e de engenharia em corpo de prova de alumínio.

Eles mostram com clareza que as diferenças entre as curvas se intensificam após o escoamento.

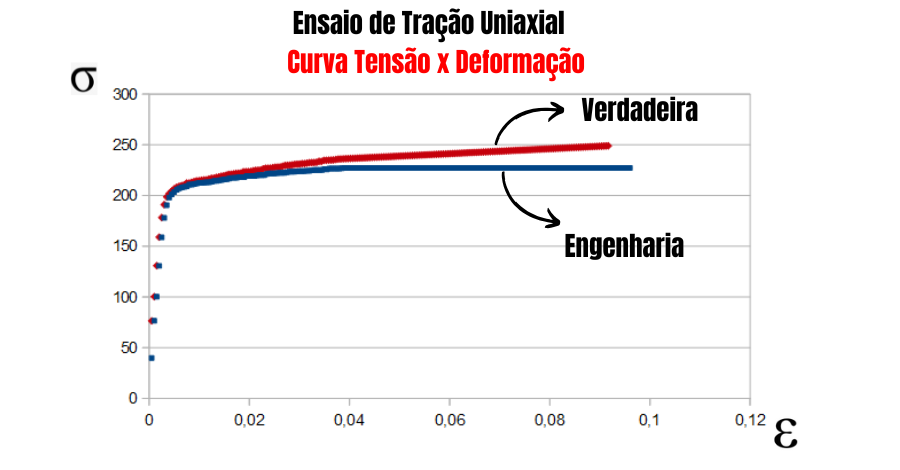
Esse tipo de análise ajuda a validar os modelos numéricos e prevê o comportamento do material em situações reais, garantindo uma avaliação mais segura, eficiente e inovadora nos projetos de componentes estruturais.

Considerações finais.

Enfim, o uso da tensão verdadeira torna possível projetar componentes estruturais e diversos produtos com maior eficiência, explorando também soluções inovadoras de forma mais refinada.

Esse recurso ainda contribui para reduzir o desperdício de materiais, elevar a qualidade final dos produtos e aumentar a confiabilidade das simulações computacionais.

Em síntese, a análise da tensão e da deformação verdadeira conecta teoria e prática, transformando resultados experimentais em avanços concretos para a engenharia moderna.

Gostou do conteúdo? Então, compartilhe este artigo com seus colegas e ajude a disseminar esse conhecimento.