Estruturas Isostáticas: Entenda os Conceitos sem Fazer Cálculos

Do ponto de vista de engenharia civil, as estruturas encontram-se em dois grandes grupos, isto é, as estruturas isostáticas e hiperestáticas.

Aliás, esses dois tipos apresentam comportamentos distintos quando submetidos à ação de carregamentos.

A escolha entre elas não é apenas uma questão teórica, mas uma decisão consciente do engenheiro na concepção estrutural. Em muitos casos, uma mesma geometria é concebida tanto como isostática quanto como hiperestática.

Logo, essa escolha influencia diretamente o modelo de cálculo adotado e pode impactar a geometria final da estrutura e, em determinadas situações, até a seleção do material estrutural.

Elementos estruturais comuns, como lajes, vigas, treliças e pilares, podem ser modelados, em contextos específicos, como estruturas isostáticas.

Portanto, compreender como isso é possível e quais são as limitações dessa modelagem é essencial para uma correta interpretação dos resultados de uma análise estrutural.

A partir do entendimento das estruturas isostáticas, desenvolve-se a base conceitual fundamental para avançar, a posteriori, no estudo das estruturas hiperestáticas e de métodos de análise mais sofisticados.

Neste artigo, o foco será apenas nas estruturas isostáticas, pois elas constituem o ponto de partida para a compreensão do comportamento estrutural de sistemas mais complexos.

O que são estruturas isostáticas?

Estruturas isostáticas são aquelas em que é possível determinar as reações de apoio e os esforços internos usando somente as equações de equilíbrio da estática.

Por essa razão, eles denominam-se também de estaticamente determinadas.

De forma geral, as equações de equilíbrio utilizadas são:

• ∑Fx = 0 → equilíbrio das forças horizontais;
• ∑Fy = 0 → equilíbrio das forças verticais;
• ∑M = 0 → equilíbrio dos momentos;

Assim, essas equações representam o equilíbrio global da estrutura e, nesses casos, são suficientes para descrever seu comportamento estrutural, sem a necessidade de recorrer a métodos mais avançados da teoria das estruturas.

Logo, a partir dessas três relações e com o número de incógnitas igual ao número de equações, logo, é possível calcular as reações de apoio nos elementos estruturais pela resolução de sistemas bem simples, assim como os esforços internos:

• Momentos fletores e/ou torsores;
• Esforços cortantes;

Implicações do comportamento isostático

O fato de uma estrutura poder ser resolvida apenas com essas equações indica que não existem apoios, ligações ou membros estruturais além do necessário para garantir o equilíbrio.

Em estruturas isostáticas, embora ocorram deformações nos elementos, elas não alteram a distribuição dos esforços internos, pois estes dependem apenas das cargas aplicadas e da geometria da estrutura.

No entanto, há uma limitação importante: a remoção de um apoio essencial influencia na perda de sua capacidade estrutural, logo, a estrutura isostática perde o seu equilíbrio global.

Logo, nessa situação, apresenta vínculos ou membros estruturais insuficientes, sendo classificada como hipostática, ou seja, torna-se um sistema instável.

Dessa forma, as estruturas isostáticas ocupam uma posição intermediária entre sistemas instáveis (hipostáticos) e sistemas com restrições adicionais, conhecidos como hiperestáticos.

A escolha de um modelo isostático liga-se à previsibilidade do comportamento estrutural e à eficiência no uso do material, dentro de hipóteses definidas.

Bem como o nível de incerteza das ligações entre os elementos estruturais e a clareza na interpretação dos resultados.

Exemplos clássicos de estruturas isostáticas

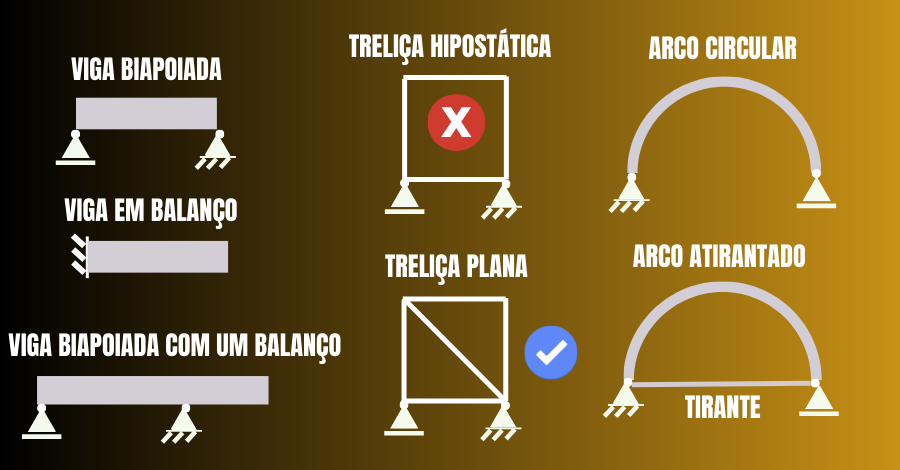
Na prática da engenharia, encontram-se poucas estruturas perfeitamente isostáticas no sentido ideal proposto pela teoria clássica.

O que se observa, na maioria dos casos, é o uso consciente de modelos isostáticos, adotados como simplificação racional para a análise e para a compreensão do comportamento global das estruturas.

Entre os exemplos mais tradicionais de estruturas isostáticas, destacam-se:

• Vigas simplesmente apoiadas;
• Vigas em balanço;
• Treliças planas;
• Arcos;

Em resumo, vamos entender mais sobre estes elementos estruturais isostáticos.

Vigas simplesmente apoiadas

Então, a viga biapoiada ocorre com mais frequência nas estruturas isostáticas, possui somente um vão e os seus apoios extremos estão em outras vigas transversais, caso tenham pequena resistência a torção.

Assim, idealizam-se os seus apoios como rótulas, o que implica momento fletor nulo nas extremidades, com liberdade de rotação e restrição ao movimento vertical.

Como consequência direta dessas condições de contorno, os esforços internos dependem apenas da geometria da viga e do carregamento aplicado.

Por exemplo, uma viga biapoiada de comprimento L, submetida a um carregamento uniformemente distribuído q, apresenta momento fletor máximo (M_max) positivo no meio do vão, dado por:

• M_max = qL²/8;

Esse resultado decorre exclusivamente das equações de equilíbrio e da configuração dos apoios, independentemente da rigidez do material ou da seção transversal.

Por outro lado, se os apoios das vigas forem pilares, existe uma rigidez rotacional, capaz de gerar momentos fletores nas extremidades, caracterizando a viga como biengastada e hiperestática.

Porém, vigas com dois apoios extremos em pilares com baixa rigidez a torção os esforços solicitantes aproximam-se de uma viga isostática.

Vigas em balanço

A viga em balanço constitui em outro exemplo clássico e bem didático de estrutura isostática.

Nesse sistema, o engaste é responsável por absorver as forças verticais e o momento fletor, enquanto a extremidade livre não impõe qualquer restrição a movimentos.

Assim, para uma viga engastada de comprimento L, submetida a um carregamento uniformemente distribuído q, a solicitação estrutural máxima concentra-se no engaste, onde ocorre o momento fletor máximo:

• M_max = qL²/2;

Esse comportamento evidencia claramente como a condição de apoio determina a distribuição dos esforços internos em estruturas isostáticas.

A propósito, em vigas de concreto armado ou metálicas, o engaste real apresenta pequenas deformações e/ou rotações.

O comportamento global permanece próximo ao idealizado, tornando o balanço um exemplo fundamental tanto do ponto de vista teórico e prático.

No entanto, é sempre necessário verificar se o apoio da viga em balanço tem rigidez suficiente para mantê-la firme em equilíbrio.

Portanto, evite usar vigas em balanço apoiadas em outras vigas, dando preferência ao uso de pilares como apoio, porém sempre com as decisões por parte do engenheiro estrutural.

Treliças planas isostáticas

Agora, um dos exemplos mais recorrentes de estruturas isostáticas é a treliça plana.

Aliás, as treliças são sistemas estruturais formados por barras retilíneas interligadas em nós, organizadas de modo a constituir apenas figuras triangulares.

A escolha da geometria triangular não é arbitrária, pois o triângulo, do ponto de vista estrutural, constitui-se na forma geométrica mais simples.

Desta forma, garante estabilidade estrutural sem a necessidade de vínculos adicionais.

Em uma treliça isostática bem configurada, as cargas aplicadas nos nós, transmitem-se ao longo das barras, exclusivamente por esforços normais de tração ou compressão.

Dessa forma, todos os esforços internos e reações de apoio podem ser determinados diretamente pelas equações de equilíbrio, sem recorrer à compatibilidade das deformações ou propriedades de material.

Esse princípio explica o uso extensivo de treliças em pontes, coberturas e torres, onde se busca vencer grandes vãos com consumo eficiente de material, mantendo previsibilidade no comportamento estrutural.

Por outro lado, a ausência ou disposição inadequada de um único elemento pode comprometer totalmente a estabilidade do sistema.

Por exemplo, uma treliça retangular ou quadrada sem diagonais transforma-se em um mecanismo incapaz de resistir a carregamentos laterais, caracterizando uma estrutura hipostática, ver Figura 2.

Em treliças, a condição isostática está diretamente associada à relação precisa entre geometria, número de barras e condições de apoio.

A presença dos arcos como estruturas isostáticas.

Outro exemplo clássico de estrutura isostática é o arco, amplamente utilizado em pontes e edificações desde a antiguidade, ver Figura 2.

O comportamento estrutural do arco baseia-se em sua geometria curva, que permite transformar cargas verticais em esforços de compressão ao longo do seu eixo.

Bem projetado, o arco transfere essas forças diretamente para os apoios, reduzindo bastante a presença de momentos fletores.

Em sua forma mais simples, com dois apoios articulados, o arco é tratado como uma estrutura isostática, cujas reações e esforços internos são obtidos exclusivamente a partir das equações de equilíbrio.

Nessa configuração, a estabilidade depende da posição dos apoios e do traçado geométrico do arco, que deve ser compatível com a linha de pressão resultante dos carregamentos.

Diferentes geometrias de arco, tais como semicirculares e arcos abatidos, apresentam comportamentos estruturais distintos, influenciando a distribuição das forças internas e os empuxos horizontais nos apoios.

Ainda assim, todos compartilham o mesmo princípio fundamental: a eficiência estrutural alcançada pela condução das cargas por compressão, com mínima redundância de vínculos.

Em resumo, o uso consciente de modelos isostáticos permite ao engenheiro interpretar corretamente o comportamento estrutural.

Portanto, estabelecer ordens de grandeza confiáveis e construir uma base conceitual sólida para análises estruturais mais avançadas.

Considerações finais

Por fim, o estudo das estruturas isostáticas exerce papel fundamental na engenharia estrutural, pois permite compreender claramente a relação entre carregamentos, geometria e condições de apoio.

Por serem sistemas estaticamente determinados, as estruturas isostáticas possibilitam a obtenção dos esforços internos e das reações de apoio exclusivamente por meio das equações de equilíbrio.

Logo, confere maior previsibilidade ao comportamento estrutural e transparência aos resultados da análise.

Embora representem uma idealização da realidade, os modelos isostáticos constituem uma ferramenta essencial, tendo em vista:

• Entendimento do funcionamento global das estruturas;
• Estimativa e ordens de grandeza dos esforços;
• Identificação de regiões críticas;

Assim, o domínio desse conceito estabelece uma base sólida para o avanço no estudo de estruturas mais complexas.

Por exemplo, a adoção consciente de modelos hiperestáticos quando as exigências de eficiência, rigidez ou desempenho estrutural assim o demandarem.

Gostou do artigo? Compartilhe com seus amigos e familiares interessados no assunto.