Vamos abordar neste artigo a armadura mínima para vigas de concreto armado, devido à ação de momentos fletores e forças cortantes.
Aliás, as vigas são projetadas para suportar cargas e transferi-las para outros elementos estruturais, como os pilares.
No entanto, a colocação de uma armadura mínima de aço é uma prática comum e essencial, mesmo quando o cálculo inicial indicar ser desnecessário.
Deste modo, você segue as diretrizes da norma brasileira, NBR-6118-2023 de concreto armado, pois é um dever do engenheiro.
Portanto, vamos entender o que é esta armadura mínima para vigas de concreto armado, os requisitos normativos e aprendermos mais com exemplos bem práticos.
O mecanismo de flexão simples em vigas de concreto armado;
Para começar, uma viga de concreto, sem armadura, depende da capacidade do concreto de resistir aos carregamentos.
No entanto, à medida que a carga aplicada aumenta, a viga se deforma e surgem tensões de tração e compressão em suas seções transversais, separadas por uma linha neutra com tensão nula.
Aliás, o concreto é bem resistente à compressão, porém, tem uma resistência à tração muito baixa.
Assim, essa combinação de forças resulta em regiões com momentos fletores e/ou esforços cortantes nas seções transversais da viga.
A propósito, esse é um mecanismo típico chamado de flexão simples, e verifica-se também em lajes e pilares.
Agora, um ponto de alerta ocorre quando a viga sai de sua “zona de conforto” e assim, alcança o limite de resistência do concreto à tração, logo, fissuras começam a surgir.
Dito isso, esse é o sinal claro que, sem armadura, a viga não pode continuar funcionando de forma segura.
Nesse primeiro cenário vamos abordar os momentos fletores e mais adiante os esforços cortantes.
Para que serve a armadura mínima para vigas?
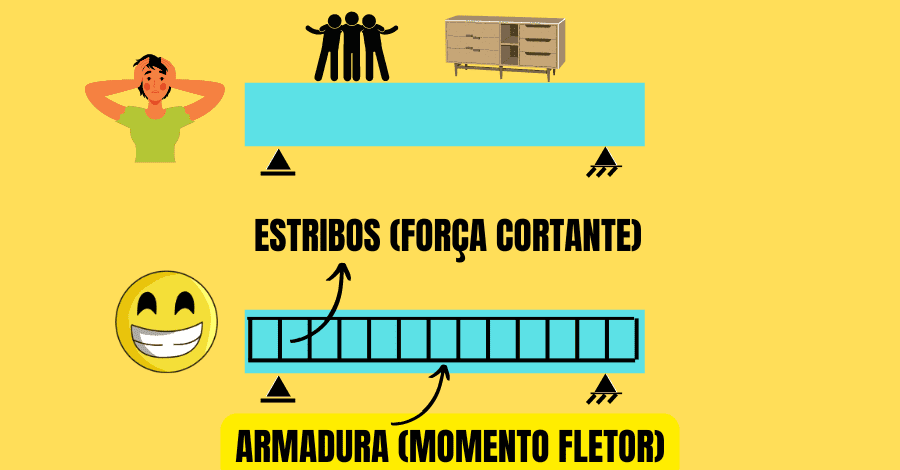
Então, a armadura mínima para vigas de concreto armado é necessária para suportar momentos fletores, e assim, não sofrer uma ruptura de forma frágil.
Logo, estabelece-se esta armadura para garantir que, em situações de estado limite último (ELU), a viga apresenta um colapso de modo dútil.
Dessa forma, a ruptura ocorre gradualmente, com a formação e propagação de fissuras e aumento de deformações.
Contudo, além de proteger contra vulnerabilidades, a armadura mínima também desempenha outro papel vital, ou seja, absorver pequenas tensões que, eventualmente, não foram consideradas no cálculo estrutural inicial.
Aliás, esses esforços podem surgir por ações de pequenas cargas acidentais ou algum outro tipo de carga que não esteja prevista no projeto estrutural.
Portanto, ela oferece uma margem de segurança adicional contra esses efeitos, logo, a viga pode resistir a pequenas tensões imprevistas sem comprometer a sua integridade.
Armadura mínima para vigas sob ação do momento fletor;
Primeiro de tudo, o cálculo da armadura mínima considera um momento fletor mínimo (Md,min), o qual é referente à fissuração da seção de concreto sem a presença da armadura.
Por essa razão, o cálculo supõe o concreto resistente a uma tensão máxima de tração, conhecida como fctk,sup, segundo a NBR-6118-2023, item 17.3.5.2, tem-se:
- Md,min = 0.8 x Wo x fctk,sup; (1)
- Wo – módulo de resistência da seção transversal da viga em relação à sua parte mais tracionada em cm3;
- fctk,sup – resistência característica superior do concreto sob a ação de tração simples, em MPa;
Em suma, na ausência de ensaios para determinar a resistência a tração do concreto (fctk,sup), a referida norma efetua um valor médio pelas equações seguintes com fck expresso em MPa :
- fctk,sup = 1,3 x fct,m; (2)
- fctk,inf = 0,7 x fct,m ; (3)
- Para concretos com fck ≤ 50 MPa: fct,m = 0,3 x (fck)⅔; (4)
- Outros casos, fck > 50 MPa: fct,m = 2,12 x ln [1+0,1x(fck+8)]; (5)
Bem, a partir do momento mínimo, usa-se um método para calcular a armadura de vigas de seção retangular, por exemplo, vamos escolher aqui a tabela “KMD”, por se tratar de um cálculo manual.
Calculando armadura mínima para vigas usando a Tabela KMD;
Bem, mediante essas etapas a seguir, chega-se ao cálculo da armadura mínima sem complicações, e a tabela encontra-se facilmente na internet.
Etapa 1: Calcular o Kc= (b x d2)/Md (cm2/KN); (6)
Onde:
b – largura da viga;
d – altura útil da viga;
Md – é igual ao momento mínimo, Equação (1)
Etapa 2: Com o valor de fck e Kc entra na tabela KMD e na linha correspondente ao valor de Kc, obtém-se o valor de Ks (cm2/KN) para o tipo de aço utilizado, por exemplo, CA-50 ou CA-60;
Etapa 3: A partir do valor de Ks obtém-se a área de armadura mínima pela equação abaixo:
As,min = (Ks x Md) / d; (7)
Portanto, a partir da equação (7) calcula-se a armadura mínima para uma viga de concreto armado, porém, temos que verificar um outro cenário.
Taxa de armadura mínima para vigas de concreto armado;
Por outro lado, a norma NBR-6118-2023 também exige que a armadura mínima respeite as taxas limites (ρmin) da tabela 17.3 para vigas de concreto armado com seção transversal retangular, onde:
ρmin = As,min/Ac; Equação (8); Ac é a área da seção transversal da viga, com largura b e altura h;
Por exemplo, na referida tabela, há:
- 20 MPa ≤ fck ≤ 30 MPa; ρmin = 0,15%;
- fck = 35 MPa; ρmin = 0,164 %;
- fck= 40 MPa; ρmin = 0,179%;
- fck = 45 MPa; ρmin = 0,194 %;
- fck = 50 MPa; ρmin = 0,208%;
Sendo assim, a partir do fck usa-se a tabela e manipulando a equação (8) calcula-se a armadura mínima (As,min) pela multiplicação de ρmin pela área da seção transversal da viga (Ac).
Vale salientar que, os valores de ρmin preveem o uso de uma armadura com aço CA-50; d/h=0,8; ४s= 1,15 e ४c= 1,4.
Veja bem, os valores do coeficiente de minoração da armadura ४s e o do concreto ४c são os tradicionais no dimensionamento de elementos estruturais de concreto armado.
Dito isso, a rigor, cabe ao engenheiro estrutural adaptar a valores diferentes ao exposto acima.
Portanto, calcula-se a armadura mínima pelo momento fletor mínimo e pela taxa de armadura, logo após, comparam-se os dois valores e adota-se o maior.
Agora, vamos ver um exemplo para esclarecer tudo o que já foi exposto.
Exemplo prático: Momento mínimo, tabelas KMD e taxa de armadura;

Então, considere uma viga de seção transversal retangular de concreto armado, com largura b=20 cm, h=60 cm, d=55 cm e fck=25 MPa e vamos seguir os seguintes passos:
Assim, no primeiro passo, deve-se calcular o Momento Mínimo:
- fct,m = 0,3 x (25)2/3= 2,565 MPa; Equação (4)
- fctk,sup = 1,3 x 2,565 = 3,334 MPa = 0,334 KN/cm2;; Equação (2)
- Wo= (20 x 602)/6 = 12000 cm3; ver Figura acima
- Md,min = 0.8 x 12000 x 0,334 = 3207 KN.cm; Equação (1)
Calcular a armadura mínima (As,min) usando a tabela KMD e o Momento Mínimo
- Kc = (20 x 552)/3207 = 18,86 cm2/KN; Equação (6)
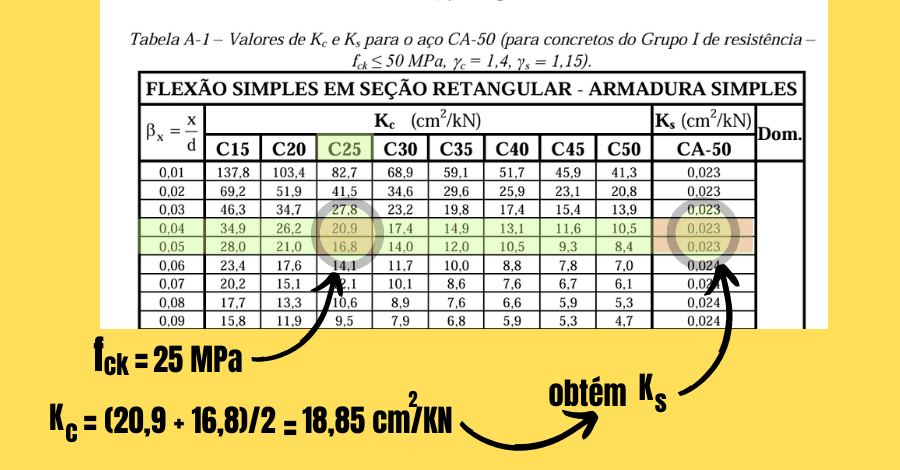
- Com os valores de Kc e fck entra na tabela KMD e obtém-se Ks igual 0,023 cm2/KN, ver Figura abaixo, para o aço CA-50;
- As,min=(0,023×3207)/55=1,35 cm2; Equação (7); Armadura Mínima
Portanto, na tabela KMD, para fck de 25 MPa, calcula-se uma média aritmética e chega-se ao valor próximo de Kc calculado na equação (6), em seguida, vai na coluna de Ks e adquire-se também o seu valor intermediário correspondente, conforme figura abaixo.
Dito isso, e para o último passo, calcular a armadura da viga com a taxa mínima, Tabela 17.3 da NBR-6118-2023;
- fck = 25 MPa; ρmin = 0,15%;
- ρmin = As,min/Ac ; Equação (8); portanto, As,min = ρmin x Ac;
- As,min = (0,15/100) x 20 x 60 = 1,8 cm2; Armadura Mínima
Portanto, como As,min calculado no passo 2 é inferior ao valor do passo 3, considera-se a armadura mínima da viga, o maior valor, ou seja, 1,8 cm2.
Agora, conforme já dito antes, vamos considerar a ação dos esforços cortantes.
Armadura mínima para vigas sob a ação de Esforço Cortante;
Aliás, a armadura transversal mínima é necessária para uma viga de concreto armado, também, para combater uma ruptura frágil e brusca.
Nesse caso, para prevenir o esforço cortante atingir um valor que provoca a fissuração diagonal do concreto.
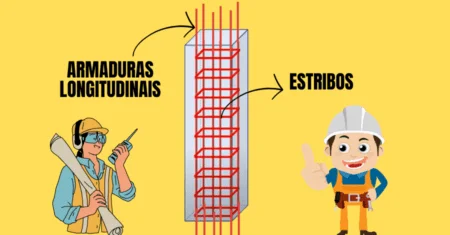
Assim, a NBR-6118-2023 estabelece os requisitos para calcular a armadura mínima e resistir às forças cortantes em seu item 17.4.1.1.1, através do uso de estribos e define uma taxa geométrica (ρsw):
ρsw = Asw / (bw × s × sen(α)) ≥ 0,2 × fct,m/fywk; (9)
Onde:
- Asw – área transversal dos estribos;
- s – espaçamento dos estribos segundo um eixo longitudinal da viga;
- bw – largura da viga;
- α – ângulo de inclinação dos estribos em relação ao eixo da viga;
- fct,m – conforme definido nas Equações (4) ou (5);
- fywk – resistência característica de escoamento da armadura;
A propósito, vamos manusear a Equação (9) considerando os estribos posicionados sempre na vertical, o mais comum, na prática, logo, adotando α=90º
Asw/s = (0,2 x fct,m/fywk) x bw x sen(90°);
Deste modo, chega-se ao cálculo direto da armadura transversal dos estribos devido à força cortante.
Asw/s = (0,2 x fct,m/fywk) x bw (cm2/cm); (10)
No entanto, precisamos definir um esforço cortante solicitante mínimo (VSd,min) e comparar com o solicitante de cálculo (VSd).
Assim, caso VSd ≤ VSd,min, ou seja, se o esforço cortante solicitante de cálculo (VSd) for inferior ao esforço cortante solicitante mínimo (VSd,min ), necessita-se considerar uma armadura mínima.
Qual o Esforço cortante correspondente à armadura mínima?
Então, adotando o modelo de cálculo I da NBR-6118-2023, admitem-se diagonais de compressão no concreto inclinadas a 45° em relação ao eixo da viga.
Aliás, primeiro verifica-se a ruptura da compressão diagonal do concreto:
VRd2 = 0,27 x αV2 x fcd x bw x d; (11)
Onde αV2 = (1-fck/250), Equação (12), com fck em unidade de MPa:
- VRd2 – esforço cortante resistente de cálculo com base nas rupturas das diagonais comprimidas de concreto, modelos indicados nos itens 17.4.2.2 ou 17.4.2.3;
- fcd – resistência de cálculo do concreto; fcd = fck/४c Equação (13)
- ४c – coeficiente de minoração do concreto armado;
Assim, necessita-se verificar as seguintes condições no Estado Limite último (ELU):
- VSd ≤ VRd2; (14)
- VSd ≤ VRd3 = Vc + Vsw; (15)
Onde:
- VRd3 – esforço cortante resistente de cálculo com base na ruptura por tração diagonal;
- Vc – parcela do esforço cortante absorvida por mecanismos adicionais à treliça;
- Vsw – parcela do esforço cortante resistida pela armadura transversal;
No entanto, o objetivo aqui é calcular o esforço cortante solicitante de cálculo mínimo (VSd,min) usando apenas o modelo I da NBR-6118-2023, o mais simples, e assim a equação (15) torna-se:
VSd,min ≤ VRd3 = Vco+ Vsw,min; (16)
Manuseando as Equações do Modelo I da NBR-6118-2023;
Para começar, vamos utilizar a primeira parcela Vco, definida segundo a norma brasileira por:
Vco = 0,6 x fctd x bw x d; (17)
Substituindo-se fctd mpor definição é fctk,inf / ४c na equação (17), o fctk,inf pela (3) e ४c = 1,4, e assim:
- Vco = 0,6 x (0,7 x fct,m /1,4) x bw x d;
- Vco = 0,3 x fct,m x bw x d; (18)
Agora, vamos tratar da segunda parcela da equação (16), Vsw,min, pelo modelo I da norma brasileira, é adaptada para condição mínima:
Vsw,min = (Asw,min /s) x 0,9 x d x fywd x (sen(α)+cos(α)); (19)
Substituindo a equação (10) na (19) e por definição, fywd=fywk/४s, para ४s=1,15 e com estribos verticais (α=90o), tem-se:
- Vsw,min = (0,2 x fct,m / fywk) x bw x 0,9 x d x (fywk/1,15) x (sen(90°)+cos(90°));
- Vsw,min = 0,1565 x fct,m x bw x d; (20)
Portanto, somando as equações (18) e (20) obtém-se a expressão do esforço cortante solicitante mínimo:
- VSd,min = 0,3 x fct,m x bw x d + 0,1565 x fct,m x bw x d ;
- VSd,min = 0,04565 x fct,m x bw x d; (21)
Ponto de atenção: a unidade de fct,m na Equação (21) é MPa e bw, d em cm, daí o resultado já sai em KN.
Cálculo da armadura de cisalhamento necessária
Então, vamos manusear de novo as Equações (16), (18), (19) para calcular a armadura necessária ao esforço cortante (cisalhamento) com estribos verticais (α=90o), s=100 cm, ४c=1.4, ४s=1.15 e aço CA-50 :
Asw / 100 = (VSd – 0.3 x fctm x bw x d)/ (0,9 x d x (50/1.15) x (sen(90o)+cos(90o)));
Asw (cm2/m) = 2.55 x (VSd / d) – 0.0766 x fct,m x bw ; (22)
Nesta fórmula (22), deve-se entrar com as unidades, fct,m em MPa, VSd em KN e bw , d em cm.
Portanto, verificam-se as seguintes condições:
- Se VSd ≤ VRd2: passou na verificação da ruptura diagonal do concreto, porém, caso contrário, alterar a seção transversal da viga ou fck até certifica-se da validação desta condição;
- Caso VSd ≤ VSd,min: Calcular a armadura mínima pela Equação (22), fazendo VSd = VSd,min, logo, nesse caso, Asw calculado já é a própria armadura mínima necessária (Asw,min).
- Para VSd > VSd,min: Calcular a armadura transversal necessária direto pela Equação (22);
Dito isso, vamos fazer um exemplo bem prático pra fixar a teoria.
Exemplo Prático de Cálculo da Armadura Transversal Mínima;
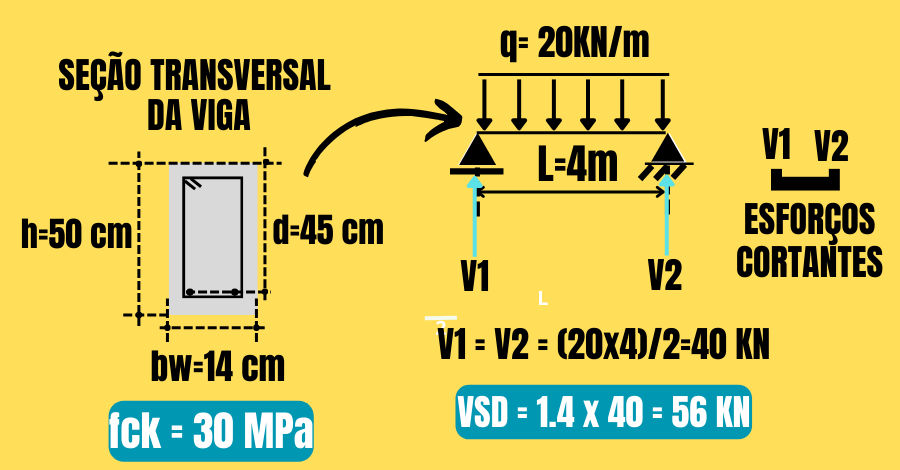
Aqui, considere uma viga de seção transversal retangular de concreto armado, com largura bw=14 cm, h=50 cm, d=45 cm, fck=30 MPa.
A propósito, como ponto de partida, verifica-se a compressão diagonal do concreto;
- αV2 = (1-30/250) = 0,88; Equação (12)
- VRd2= 0,27 x 0,88 x (3/1,4) x 14 x 45 = 320,8 KN; Equação (11)
- VSd = 56 KN; Dado do Exemplo
- Como VSd < VRd2; OK, a viga não apresenta ruptura diagonal no concreto
Na etapa seguinte, calcula-se VSd,min e compara-se com VSd fornecido pelo exemplo:
- VSd,min = 0,04565 x 0,3 x (30)2/3 x 14 x 45 = 83,30 KN; Equação (21)
- VSd = 56 KN; Dado do Exemplo
- VSd < VSd,min então, iguala VSd a VSd,min e calcula-se a armadura mínima
- fct,m = 0,3 x (30)2/3 = 2,896 MPa ; Equação (4)
- Asw,min=(2.55 x 83.3)/45 – 0.076 x 2,896 x 14 = 1.64 cm2/m; Equação (22); Armadura Mínima
Conclusão:
Em suma, a armadura mínima para vigas de concreto armado desempenha uma função crucial na segurança e durabilidade das estruturas.
Sendo assim, o papel do engenheiro é sempre checar os critérios de uso da armadura mínima, aplicar sempre que necessário, de acordo com as diretrizes da norma brasileira.
Agora, clique aqui e leia também esse artigo sobre vigas.
Sobre o Autor
2 Comentários

I’m really impressed along with your writing abilities as smartly as with the format in your weblog.
Is that this a paid subject or did you customize it yourself?
Anyway keep up the nice high quality writing, it is rare
to peer a nice weblog like this one nowadays.
Beacons AI!
the template and host are paid, however all the text is written by myself.
Regards