Armadura Dupla em Vigas de Concreto Armado sem Complicações

A armadura dupla, localizada nas faces inferior e superior de vigas de concreto armado, é calculada para resistir aos esforços típicos de flexão simples, ou seja, os momentos fletores.

Aliás, o comportamento típico de uma seção transversal em vigas de concreto armado, sob a ação de cargas, apresenta uma divisão bem definida:

• Zonas de compressão e tração;
• Linha neutra: transição entre as duas regiões;

No entanto, o concreto resiste muito bem à compressão, mas sua baixa resistência à tração exige a presença do aço, posicionado de forma estratégica na região tracionada.

Na maioria dos casos, essa configuração é suficiente para a viga resistir ao momento máximo previsto no projeto.

Por outro lado, muitos arquitetos exigem a limitação da altura das vigas em pontos estratégicos da edificação, seja por estética ou outras questões funcionais.

Além disso, a NBR 6118 estabelece limites para a relação entre a altura da linha neutra e a altura útil da viga.

Portanto, nessas situações onde deseja uma altura limitada para uma viga, mas é insuficiente para resistir ao momento fletor, a solução com armadura dupla é uma boa opção. Prossiga na leitura e compreenda.

O que é uma viga com armadura dupla?

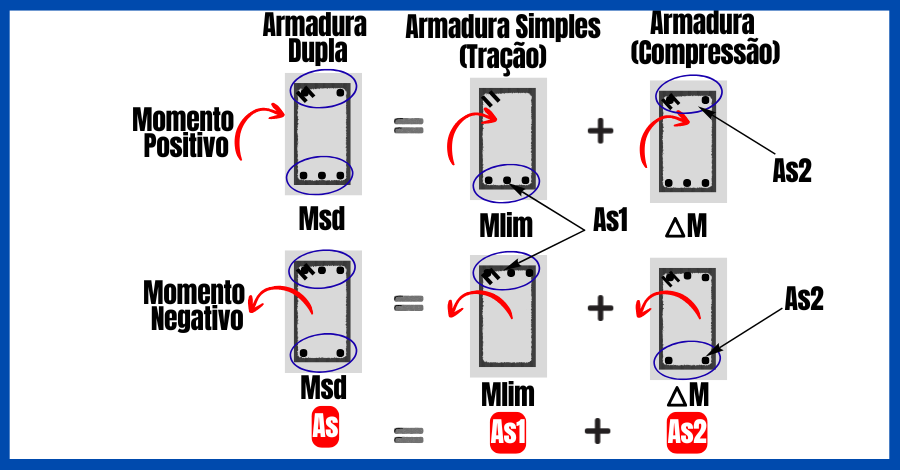
Então, define-se uma viga com armadura dupla quando ela contém aço nas regiões tracionadas e comprimidas para suportar o momento fletor solicitante.

No entanto, sem a presença da armadura de compressão, pode-se chegar uma solução com vigas de maiores alturas e passar dos limites impostos pela norma brasileira NBR 6118 em relação a x/d.

• Concreto com fck ≤ 50 MPa: x/d ≤ 0,45. (1)
• Concreto com 50 MPa < fck ≤ 90 MPa: x/d ≤ 0,35; (2)
• Altura da linha neutra: x;
• Altura útil da viga: d;

Assim, caso a viga ultrapasse esses limites, ela fica iminente para entrar no domínio 4, onde o risco de ruptura frágil é muito intenso, condição inaceitável para a segurança do projeto estrutural.

Porém, para corrigir essa situação com altura limitante, pode-se adicionar a armadura de compressão e reposicionar a linha neutra dentro dos limites estabelecidos da norma brasileira, equações (1) e (2).

Além disso, a armadura dupla torna-se uma alternativa interessante, pois permite limitar a altura da viga sem modificar outros parâmetros de projeto, tais como:

• Aumentar a resistência do concreto (fck);
• Alterar a geometria da viga (base e altura);

Por outro lado, a armadura dupla também é uma solução atrativa nos apoios internos de vigas contínuas, onde atuam momentos fletores negativos, geralmente bem maiores do que os positivos nos vãos internos.

Bem nessas regiões, a adoção de seções transversais de vigas mais altas, por exigências do dimensionamento, pode acarretar um aumento nos custos e no peso da estrutura.

Isto posto, o engenheiro estrutural pode fixar uma altura menor para a viga, introduzir a armadura dupla e atender às exigências de segurança e da norma brasileira.

Como calcular a armadura dupla em vigas?

Sobretudo, o método consiste em calcular o momento resistente máximo (Mlim) da seção transversal de uma viga somente com armadura simples e compará-lo com o momento solicitante (Msd).

• Msd = Mlim + ΔM; (3)
• ΔM = Msd – Mlim; (4)
• Msd ≤ Mlim: a solução somente com armadura de tração é suficiente;
• Msd > Mlim: existe um momento excedente (ΔM) para a armadura adicional de compressão absorver;

No entanto, vale destacar que a viga é incapaz de resistir ao aumento do momento (ΔM) apenas com adição de armadura na região tracionada.

Nesta situação, a força de tração exercida pelo aço deve equilibrar a resistência oferecida pelo concreto e pelo aço na região de compressão.

Por essa razão, acrescentar somente armadura de tração causa um desequilíbrio capaz de provocar a ruptura da viga.

Logo, o acréscimo de armadura deve ser distribuído entre as duas regiões da seção para garantir a estabilidade das forças de equilíbrio da viga.

Em resumo, considere usar uma viga com armadura dupla nessas situações principais.

• O momento fletor solicitante é bastante alto, além da capacidade de uma viga possuir somente armação simples de tração;
• As dimensões da viga não podem ser alteradas devido a restrições arquitetônicas ou de projeto estrutural;

Portanto, não é necessário alterar a geometria nem o fck do concreto.

Equações de dimensionamento em vigas de concreto armado com seção retangular

Para começar, a figura 2 representa uma viga de concreto armado com armadura dupla, seção retangular, com os diagramas de tensões, deformações e forças resultantes no aço e no concreto.

Assim, a partir das notações utilizadas, vamos definir um passo a passo para calcular a armadura dupla de uma viga de concreto armado. O significado de cada variável estão distribuídos ao longo do texto.

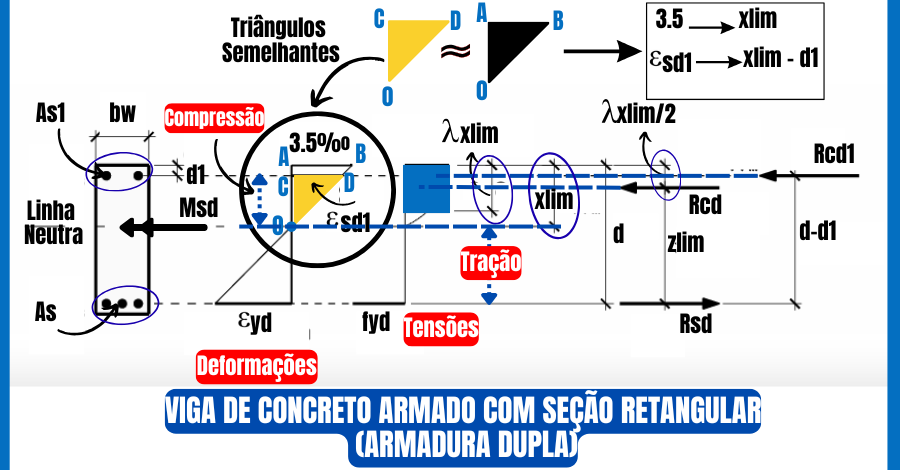
Aliás, a distribuição de tensões de compressão no concreto segue uma simplificação da norma NBR 6118, ao utilizar um diagrama retangular, item 17.2.2.e.

Deste modo, a altura do retângulo torna-se y igual a λ.x, e a tensão de pico é de ∝c.ηc.fcd, com os seguintes valores, a depender do fck do concreto:

• fck ≤ 50 MPa: λ=0.8; ∝c=0.85; (5a)
• fck > 50 MPa: λ=0.8 – (fck-50)/400; ∝c=0.85-[1-(fck-50)/200]; (5b)
• fck ≤ 40 MPa: ηc=1; (5c)
• fck > 40 MPa: ηc=(40/fck)^(1/3); (5d)

Dito isso, o primeiro passo é obter o momento solicitante (Msd), proveniente de uma análise estrutural e, em seguida, o momento limite.

Momento limite de flexão (Mlim)

Então, calcula-se o momento fletor limite em relação ao centro de gravidade (CG) da armadura de tração; Figura 2, este é o valor máximo limitante da linha neutra (xlim) nas condições fixas da norma, Equações (1) e (2).

• fcd=fck/γ_c ; γ_c=1.4, com a minoração da resistência característica fck do concreto, obtém a tensão de cálculo (fcd); (6)
• Rcd = ∝c.ηc.fcd.bw.λ.xlim; (7)
• zlim = d – λ.xlim/2; (8)
• Mlim = Rcd . zlim; (9)
• Mlim = (∝c.ηc.fcd.bw.λ.xlim) . (d-λ.xlim/2); (10)
• Rcd é força de compressão resultante no concreto;
• zlim refere-se ao braço de alavanca da força Rcd em relação ao CG da armadura de tração;

Já os parâmetros ∝c.ηc e λ são determinados pelos critérios da norma brasileira, conforme as equações (5a) a (5d).

Nessa situação, somente se leva em conta a força de compressão no concreto para calcular o momento limite, fronteira do uso de armadura de tração.

Tensões (σ_sd1) e deformações (Ɛ_sd1) no concreto comprimido

Através de um artifício simples de semelhança de triângulos (OCD e OAB), pelo diagrama de deformações no concreto armado (ver Figura 2), determinam-se as tensões e deformações do concreto sob compressão.

• Ɛ_sd1 = 0.0035.(xlim-d1)/xlim; (11)
• Ɛ_sd1 < Ɛyd: σ_sd1=Es.Ɛ_sd1; (12)
• Ɛ_sd1 ≥ Ɛyd: σ_sd1=fyd; (13)
• d1=cob+Ф_E+Ф_L/2; (14)
• Es – módulo de elasticidade do aço igual a 210 GPa, com ausência de ensaios experimentais ou sem os dados do fabricante segundo a NBR-6118;
• d1 é a distância do centro de gravidade da armadura de compressão a face mais próxima da viga;
• cob refere-se ao cobrimento do concreto, Ф_L e Ф_E, os diâmetros da armadura de compressão e do estribo;

Assim, a deformação de escoamento do aço (Ɛyd) é determinada pela divisão entre a tensão de escoamento de cálculo do aço (fyd=fyk/γs ; γs=1.15) e o módulo de elasticidade do aço (Es), já fyd é a tensão de escoamento característica do aço.

Momento excedente (ΔM): adotar armadura dupla somente se ΔM > 0.

Agora, de posse de Mlim, verifica se existe um momento excedente (ΔM), a partir da diferença entre o momento solicitante (Msd) e o momento limite (Mlim).

• ΔM = Msd – Mlim; (15)
• ΔM ≤ 0 – não é necessário usar armadura dupla, somente no caso contrário, ou seja, ΔM > 0.
• Rcd1 = As1.σ_sd1; (16)
• ΔM = Rcd1 . (d-d1) = As1.σ_sd1. (d-d1); (17)
• As1 = ΔM / (σ_sd1. (d-d1)); (18)
• As1 – área de armadura comprimida;
• Rcd1 – força resultante sob compressão na armadura;
• σ_sd1 – tensão de compressão na armadura;

Portanto, de acordo com a equação (18), determinar-se o valor da área da armadura de compressão (As1), e com o valor de ΔM calculado pela distância da força de compressão (Rcd1) em relação ao centro de gravidade da armadura de tração.

Armadura de Tração (As)

Tendo em vista o equilíbrio de forças na seção transversal de uma viga de concreto armado com armadura dupla, e usando as Equações (7) e (16):

• Rsd = Rcd + Rcd1; (19)
• Rsd = As.fyd; (20)
• As.fyd = ∝c.ηc.fcd.bw.λ.xlim+As1.σ_sd1; (21)
• As = (∝c.ηc.fcd.bw.λ.xlim+As1.σ_sd1)/fyd; (22)

Assim, através das equações (18) e (22), obtém-se as armaduras de tração e compressão de uma viga de concreto armado com armadura dupla. Pontos de atenção:

• Se ΔM for muito pequeno, a armadura de compressão não pode ser inferior à mínima exigida pela norma NBR-6118.
• Se a altura da viga ainda ficar elevada com armadura dupla, avalie alterar a altura ou o fck do concreto ou ainda reavaliar a estrutura lançada.
• Verificar a ancoragem, os espaçamentos das armaduras e os estados limites de serviço e fissuração, logo após o dimensionamento da viga.

Exemplo: Flexão Simples em Vigas de Concreto Armado com Armadura Dupla

Então, vamos utilizar os dados de uma viga hipotética, com seção retangular de 20 cm (bw) x 40 cm (h), e os esforços solicitantes definidos no pórtico espacial do software TQS, conforme a figura abaixo.

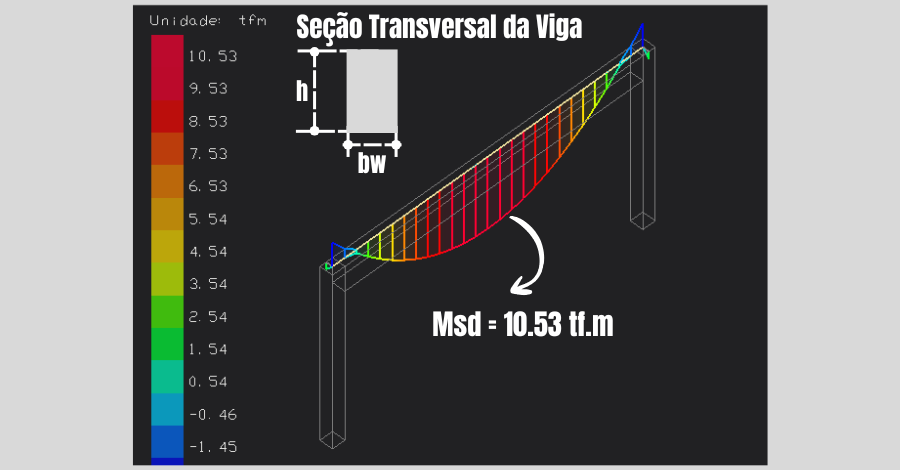
Assim, calcule as armaduras necessárias para a viga e verifique a condição de uso de armadura dupla com os seguintes dados:

• fck = 20 MPa;
• fyk = 500 MPa; (CA50)
• cob=3 cm;
• ४s=1,15;
• ४c=1,4;
• Msd = 10.53 tf.m;
• L = 5 m;

Primeiro passo: Determinar os parâmetros λ, ∝c, ηc , fcd, d, d1 e xlim:

• fck = 20 MPa: λ=0.8; ∝c=0.85; ηc=1;
• fcd = 200/1.4 = 142.86 Kgf/cm²;
• Ф_E = 5 mm; Ф_L = 10 mm. (Condição inicial)
• d1=cob+Ф_E+Ф_L/2 = 3 + 0.5 + 0.5 = 4 cm;
• d= h – cob – Ф_E – Ф_L/2 = 40 – (3 + 0.5 + 0.5) = 36 cm;
• xlim = 0.45.d = 0.45.36=16.2 cm;

Segundo passo: Calcular o momento limite, ou seja, até aqui não uso armadura dupla:

• Rcd = ∝c.ηc.fcd.bw.λ.xlim =(0.85).1.(142.86).20.(0.8).(16.2)= 31.47 tf;
• zlim = d – λ.xlim/2 = 36 – (0.8).16.2/2 = 29.52 cm;
• Mlim = Rcd . zlim = (31.47).(29.52) = 9.29 tf.m;

Terceiro passo: Verificar se necessita de armadura dupla

• ΔM = Msd – Mlim = 10.53 – 9.29 = 1.24 tf.m, ΔM > 0 (sim);

Quarto passo: Calcular as tensões e deformações de compressão

• Ɛ_sd1 = 0.0035.(xlim-d1)/xlim = (0.0035).(16.2-4)/16.2 = 0.0026;
• fyd = fyk/४s=5000/1.15 = 4348 Kgf/cm²;
• Es = 210000 MPa;
• Ɛyd = fyd/Es = 4348/2100000 = 0.00207; (Ɛsd1 > Ɛyd)
• Ɛsd1 ≥ Ɛyd: σ_sd1=fyd = 4348 Kgf/cm²;

Quinto passo: Calcular a armadura de compressão

• As1 = ΔM / (σ_sd1. (d-d1)) = 124000 / (4348.(36-4));
• As1 = 0.89 cm²;

Sexto passo: Calcular a armadura de tração

• Rcd1 = As1.σ_sd1 = (0.89).(4348)= 3.87 tf
• As = (Rcd + Rcd1)/fyd = (31470+3869.72)/4348;
• As =8.13 cm²;
• Rsd = As.fyd = (8.13).(4348) = 35.35 tf;

Portanto, este exemplo ilustrativo mostrou um passo a passo para o cálculo manual da armadura dupla de uma viga de seção retangular de concreto armado.

Logo, veja na figura abaixo que os resultados das armaduras (As e As1) e resultante de forças de tração (Rsd) e compressão (Rcd e Rcd1) equivalem aos resultados da calculadora do TQS.

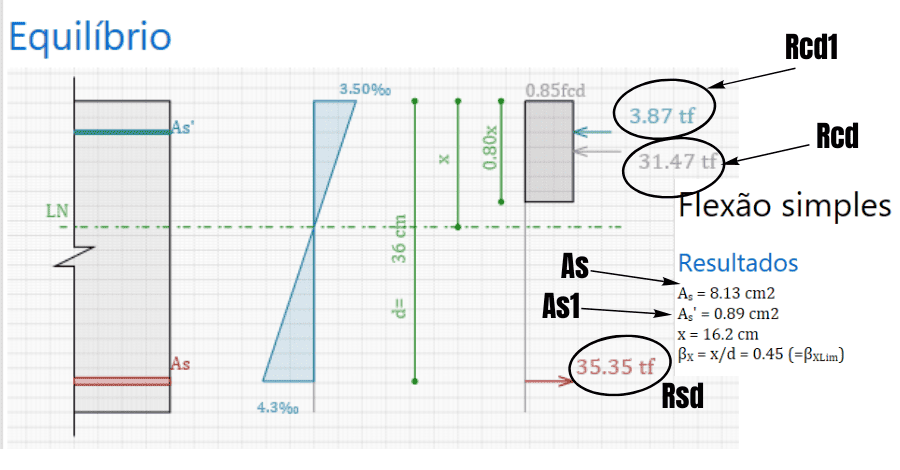
Considerações Finais

Então, as vigas de concreto armado com armadura dupla se apresentam como uma solução eficiente em situações onde a altura da viga é um fator limitante.

Aliás, a inclusão de barras de aço na região comprimida garante o equilíbrio entre as forças de tração e de compressão.

Portanto, a viga será capaz de suportar a momentos fletores além do limite (x/d) sem o risco de ruptura frágil.

Nesse cenário, eia também esse artigo complementar sobre flexão simples em vigas de concreto armado sem armadura de compressão.