Viga t de Concreto Armado: Entenda os Aspectos Básicos da Teoria (Parte 1)

As seções transversais em vigas de concreto armado podem assumir diferentes formas geométricas, dentre elas, destacam-se as retangulares, circulares e a viga t.

Aliás, a viga t surge quase naturalmente nas estruturas usuais de concreto armado, como resultado da ação solidária entre as vigas e suas lajes vizinhas em estruturas de edifícios e pontes.

Ela aparece com frequência maior do que se imagina e nem sempre são exploradas de forma consciente no dimensionamento das vigas.

Assim, entender essa interação no cálculo estrutural é parte essencial de um projeto mais seguro, racional e fundamentado no amplo conhecimento do engenheiro estrutural.

Portanto, vamos aprender mais detalhes sobre a viga t de concreto armado, parte 1, sob a ótica de projetos estruturais, com ênfase nos aspectos básicos da teoria.

O que é viga t de concreto armado?

Então, o nome deriva do formato em letra T da seção transversal da viga, composta por uma mesa, parte ampliada da largura da seção, e uma nervura, responsável pela maior parcela da altura resistente (perna do T).

A consideração da seção da viga t no dimensionamento depende dos seguintes aspectos:

• Posição da linha neutra na viga;
• Posição da laje em relação à viga (superior ou inferior);
• Sinal do momento fletor atuante (positivo ou negativo);

Aliás, a interação entre viga e laje de concreto armado decorre do comportamento do conjunto sob a ação da flexão.

Assim, as tensões normais de compressão geradas em determinadas regiões da viga não se limitam à sua largura, podendo se distribuir para a laje ao lado da viga.

Porém, desde que exista continuidade geométrica e adequada solidarização entre os elementos estruturais.

A laje contribui para a resistência da viga quando posiciona-se na região comprimida da seção, pois o concreto tem elevada resistência à compressão.

Deste modo, a participação da laje amplia a zona de compressão em um trecho limitado da seção e altera o modelo resistente da viga.

Por outro lado, caso a laje esteja posicionada na região de tração da viga, sua contribuição estrutural torna-se desprezível devido à baixa resistência do concreto à tração.

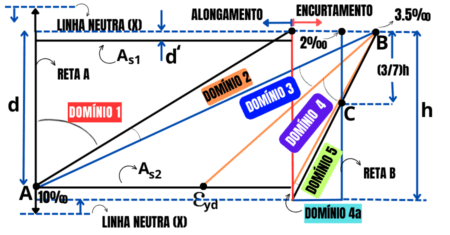
Portanto, a posição da linha neutra como divisão das zonas de tração e compressão também na viga t exerce um papel preponderante, embora esse formato de geometria seja imperceptível visualmente após a execução da estrutura.

Posição da laje e sinal do momento fletor da viga

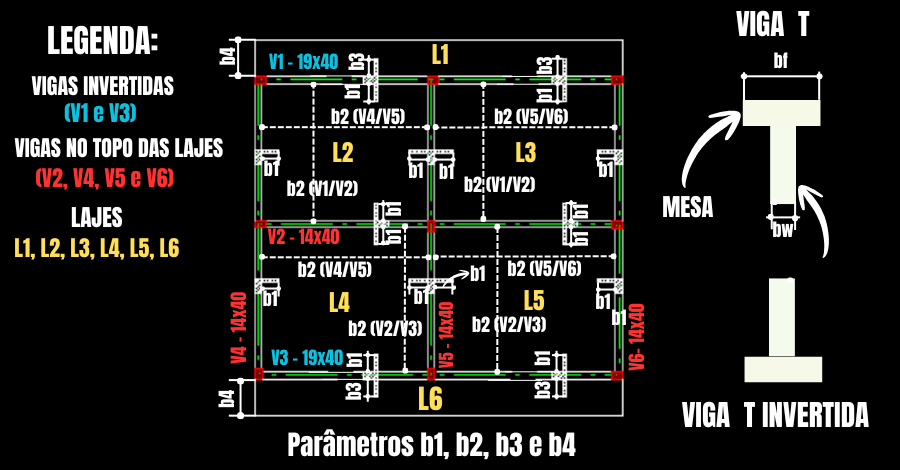
Na maioria das estruturas de concreto armado, a laje posiciona-se na parte superior da viga, por exemplo, vigas V2, V4, V5 e V6 (ver Figura 1).

Assim, reforça-se a contribuição da laje para a formação da seção t nos trechos da viga submetidos a momentos fletores positivos.

No entanto, situações comuns de projeto estrutural também ocorrem com a laje posicionada na parte inferior da viga, como nos casos de vigas invertidas V1 e V3 (Figura 1).

Nessa configuração, a adoção de vigas em t torna-se mais adequada nos trechos submetidos a momentos fletores negativos, pois a região comprimida da viga localiza-se abaixo da linha neutra.

Ainda assim, por razões de modelagem, detalhamento e execução, é comum considerar a seção t ao longo de todos os vãos das vigas.

Acima de tudo, o engenheiro estrutural avalia essa simplificação e verifica a coerência do ponto de vista da segurança estrutural e da economia de materiais.

Portanto, a consideração da seção t possibilita melhor aproveitamento do concreto sob compressão, redução da taxa de armadura longitudinal e maior controle das deformações das vigas.

Largura colaborante da laje em viga t

Então, esta refere-se à faixa efetiva da laje que realmente participa do mecanismo resistente à compressão da viga t, na mesa da viga.

No entanto, embora a laje possa apresentar uma largura muito maior, apenas uma parte limitada é efetiva, pois as tensões de compressão tendem a diminuir a medida que que se afasta da nervura da viga.

Aliás, a participação da laje na resistência à flexão de viga t exige uma ligação estrutural para transmitir as tensões de cisalhamento desenvolvidas na interface entre a mesa e a nervura.

Assim, essas tensões mobilizam a compressão na laje e a transferem para a nervura da viga, garantindo o comportamento solidário da viga t.

Logo, em situações usuais de projeto, essa condição exige a presença de armaduras específicas de ligação entre a laje e a viga, denominadas armaduras de costura.

Portanto, a ausência ou detalhamento inadequado dessas armaduras pode comprometer a transferência de esforços, pois reduz a contribuição efetiva da mesa e a validade do modelo de viga t adotado na análise à flexão.

Cálculo da largura (bf) em viga t segundo a NBR-6118

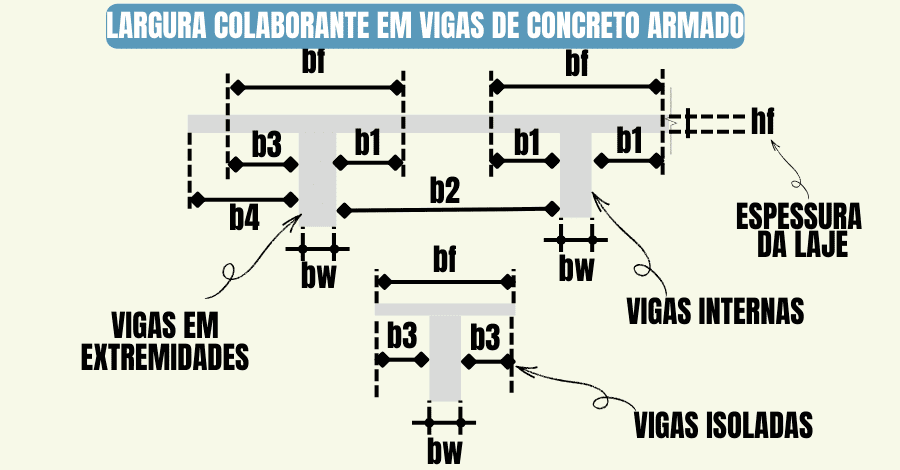
Então, a norma apresenta um cálculo simplificado para determinar a largura colaborante da laje (bf), definida a partir da largura da nervura da viga (bw), acrescida de uma parcela extra das lajes adjacentes (b1, b2, b3 e b4), Figura 2.

Assim, a norma brasileira define estas variáveis; porém, neste artigo, vamos nos concentrar nos seguintes casos:

• Sem adotar mísulas: saliências inclinadas no canto entre a nervura e a mesa das vigas;
• Ausência de aberturas nas lajes;

Logo, essas parcelas não devem ultrapassar, em cada lado da viga onde existe a laje colaborante, as seguintes relações:

• b1 ≤ (0.5) x b2 e b1 ≤ (0.1) x a; (1)
• b3 ≤ b4 e b3 ≤ (0.1) x a; (2)

Nesse caso, o valor de (a) refere-se ao limite correspondente a 10% da distância entre dois pontos sucessivos de momento fletor nulo.

Já a variável b2 refere-se à distância interna entre vigas; b4 é o comprimento do vão de uma viga em balanço. Assim, calcula-se b1 ou b3 de acordo com as equações (1) e (2), adotando-se o menor valor.

Portanto, com base na posição da viga na estrutura, obtém-se o valor da largura colaborante (bf):

• Vigas nas extremidades: bf = bw + b1 + b3; (3)
• Vigas internas: bf = bw + b1 + b1; (4)
• Vigas isoladas: bf = bw + b3 + b3; (5)

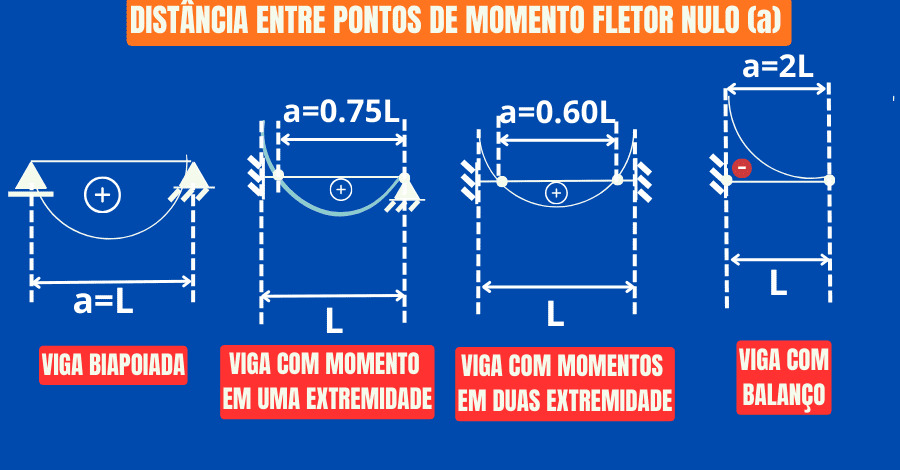
Definição do parâmetro (a) pelo diagrama de momentos fletores

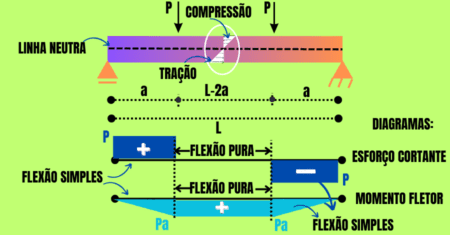
Por outro lado, a NBR-6118 estabelece o valor dessa distância(a) conforme as condições de apoio e comprimento do vão da viga (L); veja a Figura 3:

• Vão com momentos nulos nas extremidades: a = L;
• Vão com um momento em uma extremidade: a = (0.75).L;
• Vão com momentos em ambas as extremidades: a = (0.60).L;
• Vão com um balanço: a = 2.L;

No entanto, a referida norma também enfatiza outra maneira de calcular esta distância (a), ou seja, mediante os diagramas de momentos fletores das vigas no projeto estrutural em questão.

Para vigas contínuas, permite-se um único valor de largura colaborante ao longo de toda a viga, inclusive nas regiões de apoio com momentos negativos.

Neste caso, determina-se o valor do trecho de momento positivo mais desfavorável, em que a largura colaborante calculada seja mínima.

Exemplo de cálculo da largura colaborante da laje em viga t

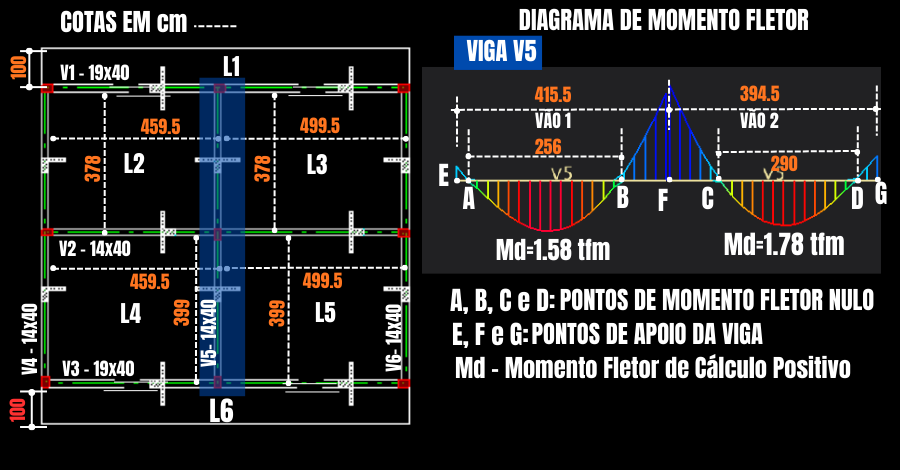
Considere a estrutura hipotética ilustrada na Figura 4, composta por lajes, vigas e pilares, modelada no software TQS.

Assim, deseja-se determinar a largura colaborante da viga V5 (bf), cuja largura (bw) igual a 14 cm, situada entre duas lajes adjacentes, L2 e L3. Os vãos entre eixos das lajes são:

• Laje L2: L = 473.5 cm;
• Laje L3: L = 513.5 cm;

A viga V5 é contínua, com dois vãos entre apoios:

• Vão EF (vão 1): L = 415.5 cm;
• Vão FG (vão 2): L = 394.5 cm;

Os momentos fletores de cálculo positivos são:

• Vão 1: Md = 1.58 tf·m;
• Vão 2: Md = 1.78 tf·m;

Como a viga V5 é interna e possui lajes em ambos os lados, determina-se a largura colaborante conforme os critérios da NBR 6118, por meio dos parâmetros a, b1 e b2, definidos nas Figuras 2 e 3.

Logo, para vigas internas, aplicam-se simultaneamente as seguintes limitações:

• b1 ≤ (0.5) x b2 e b1 ≤ (0.1) x a; (6)

Determinação dos parâmetros b1, b2, a da viga t

Então, primeiro obtém-se o parâmetro b2 a partir da distância entre os vãos internos das lajes, entre vigas, Equação(6):

• Laje L2: b2 = 459.5 cm; b1 ≤ 0,5 × 459.5 cm; b1 ≤ 229.75 cm;
• Laje L3: b2 = 499.5 cm; b1 ≤ (0,5) × 499,5 cm; b1 ≤ 249.75 cm;

Após determinar o primeiro valor de b1, calcula-se a distância entre os pontos de momento fletor nulo (a), admite-se duas formas pela NBR 6118:

• Caso 1: Vigas com momentos fletores nas duas extremidades do vão, pode-se adotar: a = (0.60) x L;
• Caso 2: Diagrama real dos momentos fletores da viga;

No primeiro caso, aplicando-se ao vão da viga V5:

• Vão 1: a = 0.6 × 415.5; a = 249.3 cm;
• Vão 2: a = 0.6 × 394.5; a = 236.7 cm;

No segundo caso, pelo software TQS gerou-se o diagrama do momento fletor real da viga e os pontos de momento fletor nulo (Figura 4).

• Vão 1: a = 256 cm;
• Vão 2: a = 290 cm;

De acordo com a NBR 6118, considera-se para o cálculo da largura colaborante (bf) o vão com momento fletor positivo mais desfavorável.

Portanto, pela figura 4, o vão 2 da viga V5 apresenta o maior valor de momento positivo (Md = 1,78 tf·m); logo, torna-se o vão determinante.

Dito isso, aplica-se o critério mais restritivo (b1≤0.1xa) para o vão 2 da viga V5, pois o primeiro critério (b1≤0,5×b2) apresenta valor bem superior, e obtém-se:

• Caso 1: b1 ≤ 0.1 × 236.7 cm; b1 = 23 cm.
• Caso 2: b1 ≤ 0.1 x 290 cm b1 = 29 cm;

Soluções para valores de largura colaborante (bf) da viga t

Diante desse cenário, a utilização do diagrama real de momentos fletores leva a uma maior largura colaborante:

• Caso 1: bf = bw + 2 x b1; bw = 14 + 2 x (23); bf = 60 cm;
• Caso 2: bf = bw + 2 x b1; bf = 14 + 2 x (29); bf = 72 cm;

A propósito, essa abordagem representa uma avaliação mais realista da extensão da região comprimida da viga sob flexão positiva.

Embora resulte em uma largura colaborante maior, trata-se de um procedimento mais seguro e realista com o diagrama de momento fletor real da viga.

Considerações finais

Este artigo apresentou os fundamentos teóricos relacionados à consideração da viga t em estruturas de concreto armado, parte 1, com ênfase na definição da largura colaborante da laje (bf), conforme os critérios estabelecidos pela NBR 6118.

Assim, você aprendeu os mecanismos físicos que justificam a colaboração da laje na viga, bem como os parâmetros normativos para determinar a geometria da viga t.

Sobretudo, a adoção da viga t constitui uma decisão de projeto que deve ser tomada de forma consciente pelo engenheiro estrutural.