Viga em Balanço: Asas para a Criatividade

Agora preste atenção, um elemento estrutural comum na engenharia civil é a viga em balanço.

Sendo assim, ela encontra-se em várias estruturas ao nosso redor, como varandas de apartamentos ou casas, fachadas, telhados e pontes.

Então, o que torna a viga em balanço tão especial? Bem, seu projeto estrutural é bastante desafiador para o engenheiro, em caso de grandes vãos e carregamentos acentuados.

Sendo assim, para entender melhor a dificuldade com os balanços, você pode estender um braço e segurar uma bandeja na palma da mão.

Porém, com ela vazia é seguro, mas à medida que se adiciona mais peso, fica mais difícil de mantê-la firme com o braço esticado, pois ele pode fazer o movimento descendente e até derrubar a bandeja no chão.

Portanto, este é o grande desafio dos balanços, mantê-los firmes e retos, sob a ação de cargas e com apenas um apoio.

Com isso em mente, vamos descobrir os segredos de uma viga em balanço, como conceitos, carregamentos, esforços e muito mais por aqui. Vamos começar a leitura?

O que é uma Viga em Balanço?

Bem diferente de outras vigas convencionais, que têm dois ou mais apoios, a viga em balanço sustenta-se em apenas uma extremidade, enquanto a outra fica livre.

Logo, esta viga especial tem uma característica peculiar, pois é fácil perceber sua distinção, em relação a outros tipos de vigas, e também adiciona elementos estéticos únicos na arquitetura.

Agora, uma das principais vantagens das vigas em balanço é ampliar o seu vão, sem a necessidade de pilares, ou estruturas de suporte, em locais onde é importante manter os espaços vazios.

Sendo assim, ao estender a viga a partir de um único ponto de apoio, não há interrupção na navegação ou tráfego embaixo.

A propósito, o projeto torna-se bem mais criativo e atraente, já que oferece a capacidade de criar estruturas,com projeções fora da linha principal da construção.

Tudo isso tem um limite?

Sim, pois existe a restrição de carregamentos, deslocamentos e extensão do balanço.

Em alguns casos, a execução na obra pode ser mais complexa, com a necessidade de técnicas especiais ou suporte temporário, durante o processo construtivo.

Dito isso, os materiais mais comuns para utilização de vigas em balanço são:

• Concreto Armado;
• Concreto Protendido;
• Aço Estrutural;
• Madeira;

Por outro lado, o comportamento estrutural do balanço não é o mesmo que de outros tipos de vigas, pois ter uma extremidade livre em uma borda, permite que a viga se mova de forma mais fácil.

Desse modo, os carregamentos mais comuns presentes em uma viga em balanço provém do seu próprio peso e de alvenarias, reações de laje, e até cargas concentradas de vigas ou outros elementos estruturais.

Portanto, sob a ação de cargas verticais uniformes ou concentradas, ela encurva-se e desloca-se para baixo, sendo assim, o maior deslocamento e rotação ocorre na extremidade livre.

No entanto, esse movimento é influenciado por vários fatores, tais como:

• Tipo do Material,
• Geometria da seção transversal;
• Intensidade das cargas aplicadas;
• Tamanho do Vão;

Sendo assim, essa curvatura gera forças de tração nas fibras superiores, muito mais acentuada nas regiões próximas ao apoio e compressão nas fibras inferiores.

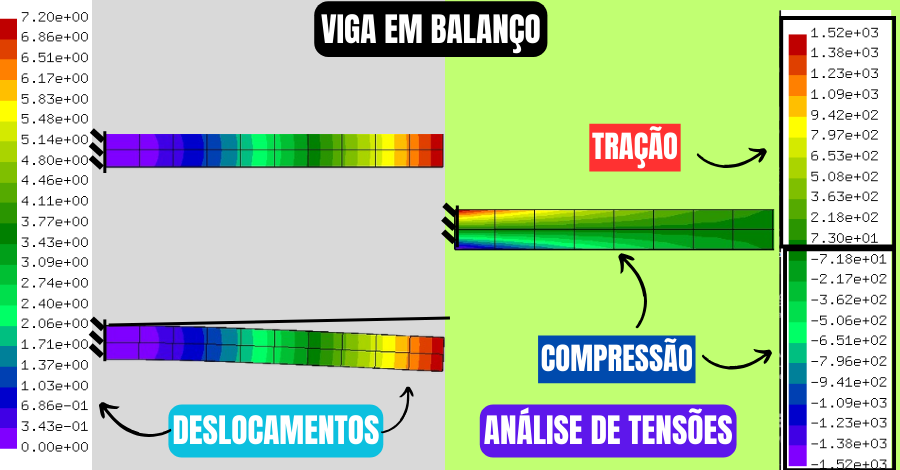
Cálculo Manual dos Esforços de Viga em Balanço Simples;

Então, as vigas em balanço estão sujeitas aos esforços, que surgem devido à aplicação de cargas externas e às condições de engaste, em seu único apoio, tais como:

• Momento Fletor: máximo no ponto de fixação da viga e diminui em direção à extremidade livre;
• Força Cortante: responsável por manter o equilíbrio vertical dos segmentos da viga. A sua magnitude varia ao longo do comprimento, sendo maior no apoio.

Dito isso, calcular os esforços cortantes e momentos fletores envolve analisar a distribuição de cargas, e aplicar as equações de equilíbrio.

Logo, assume-se também que um dos apoios é um suporte fixo, ou seja, sem qualquer tipo de rotação ou translação em qualquer direção.

Sendo assim, a soma das forças verticais e momentos é ajustada para zero, para obter as reações e os momentos fletores.

A partir daí, constroem-se os diagramas de esforços, pois eles fornecem as representações visuais de como as forças cortantes e momentos fletores variam ao longo do comprimento da viga.

Por exemplo, tem-se uma viga em balanço com carga distribuída uniforme ao longo do vão, e uma carga concentrada na extremidade, Figura 3, tem-se as seguintes etapas:

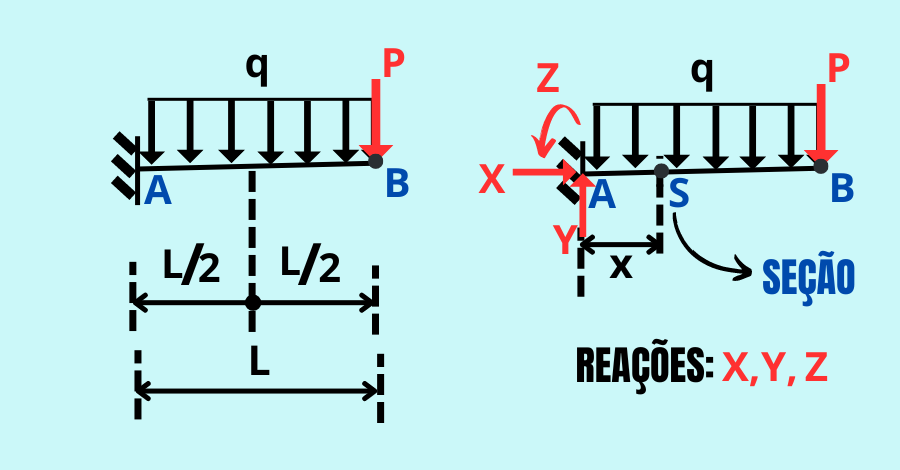
Orientação dos Eixos da Viga :

• Direção x: horizontal ao longo do eixo da viga;
• Direção y: vertical, ortogonal ao eixo da viga;

Cálculo das Reações de Apoio da Viga em Balanço;

• Passo 1: Somatório das forças na direção horizontal igual a zero.
• ∑F_H=0;
• X=0;
• Passo 2: Somatório das forças na direção vertical igual a zero.
• ∑F_V=0;
• Y-q.L-P=0; Y=P+q.L;
• Passo 3: Somatório dos momentos em relação ao ponto de apoio A, igual a zero. Considera-se os momentos positivos que giram no sentido horário.
• ∑M=0;
• -Z+P.L+qL²/2 = 0; Z=P.L+q.L²/2;

Dessa forma, obtiveram-se as reações de apoio (X), (Y) e o momento fletor (Z), e em seguida vem os diagramas dos esforços.

Diagramas de Esforço Cortante e Momento Fletor;

Agora, considera-se uma seção S a uma distância x do apoio, conforme Figura 3, e a equação do momento fletor (M) é obtida pela multiplicação das forças verticais à esquerda da seção pelas suas respectivas distâncias, mais a adição ou subtração do momento fletor, conforme o seu sentido de giro:

• M(x)=(P+q.L).x-q.x²/2-(P.L+q.L²/2); (1)
• x=0; M=-(P.L+q.L²/2);
• x=L; M=0;

Por outro lado, o esforço cortante (Q) obtém-se pela derivada da Equação (1) do momento fletor:

• Q(x)=dM/dx; Q(x)=(P+q.L)-q.x; (2)
• x=0; Q=P+q.L;
• x=L; Q=P;

Depois de tudo, a partir da solução deste problema, vamos obter, de modo simples, os diagramas de mais duas situações:

Caso 1: Somente com carga concentrada na ponta do balanço.

• q=0 nas Equações (1) e (2):
• Momento Fletor: M(x)=P.x-P.L (3)
• Esforço Cortante: Q(x)=P; (4)

Caso 2: Somente com carga distribuída ao longo do vão.

• P=0 nas Equações (1) e (2):
• Momento Fletor: M(x)=q.L.x-q.x²/2-q.L²/2; (5)
• Esforço Cortante: Q(x)=q.L-q.x; (6)

Sendo assim, a partir das Equações (1) a (6) constroem-se os diagramas de esforço Cortante e Momento fletor, conforme Figura 4 abaixo.

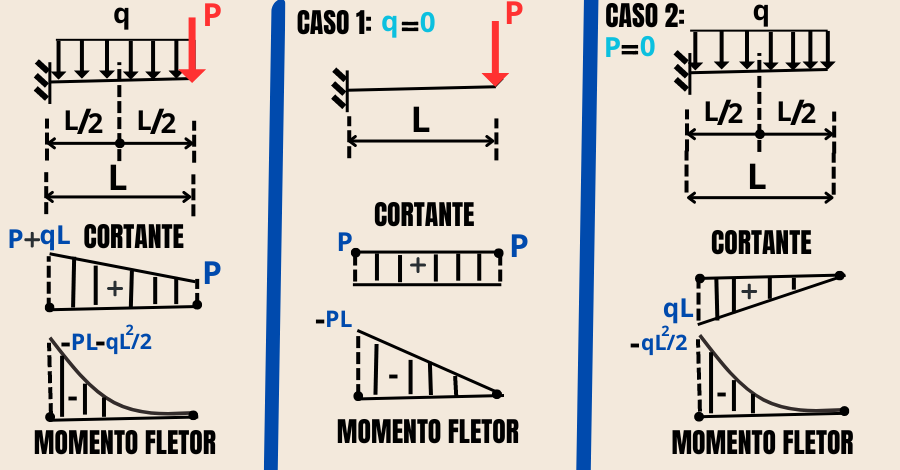
Agora, vamos para um caso particular de viga, muito utilizada na construção civil, e entender quais as suas principais armaduras,

Armadura de Viga em Balanço em Concreto Armado;

A propósito, as principais armaduras presentes são projetadas para lidar com os esforços, que atuam de forma bem diferente, em comparação com uma viga biapoiada.

Aqui está um resumo das armaduras provenientes em uma viga em balanço:

• Armadura Superior (Negativa): essencial para lidar com as tensões de tração que ocorrem na parte superior da viga, em especial na região do apoio, onde deve está bem ancorada.
• Armadura Inferior (Positiva): está sob compressão, e funciona mais com um porta estribos no balanço, para manter os estribos e a armadura superior, nos seus devidos lugares;
• Estribos: resistir aos esforços de cisalhamento;

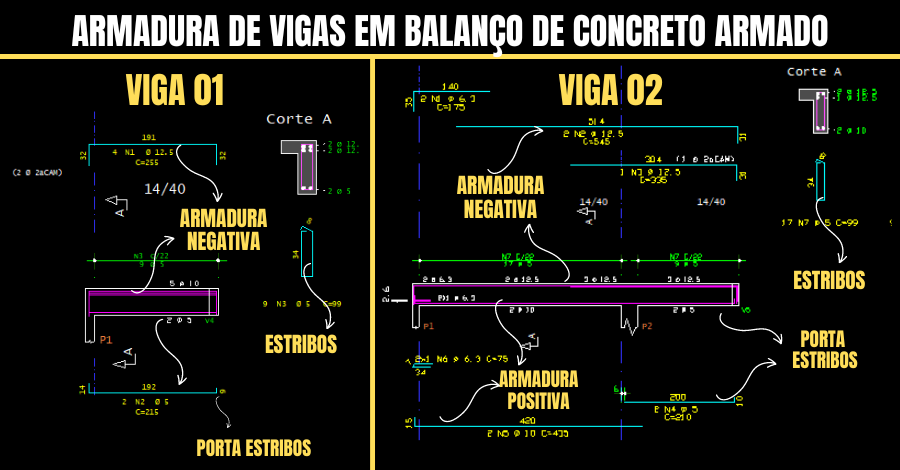
Portanto, essas armaduras são essenciais para garantir sua estabilidade estrutural e capacidade de suportar cargas de maneira eficiente.

Pontos de Atenção para Viga em Balanço;

Então, considere duas vigas com comprimentos iguais, elas se deformam muito mais do que elementos com apoios, como vigas biapoiadas ou contínuas.

Sendo assim, vamos assumir uma viga de comprimento L, com suporte fixo em ambas as extremidades, sob uma carga uniforme descendente (q), portanto, ela terá um deslocamento (δ₁) e momento fletor positivo (M_max), máximos no meio do vão:

• δ₁=5.q.L⁴/(384. E.I);
• M_max=q.L²/8;

Onde: E — Módulo de elasticidade do material, I — Momento de inércia da seção transversal;

Por outro lado, com essa mesma viga, remove-se um apoio e engasta a outra extremidade, então o deslocamento máximo (δ₂), na ponta do balanço, e o momento máximo negativo no engaste (M_eng) serão:

• δ₂=q.L⁴/(8.E.I);
• M_eng=-q.L²/2;

Logo, a viga em balanço se deforma em torno de 10 vezes mais em relação à viga com dois apoios simples.

Por outro lado, em termos de seção transversal, o momento no balanço é quatro vezes superior, e é por isso que as deformações e os esforços são predominantes para o seu dimensionamento estrutural.

Como Amenizar Estes Efeitos?

Então, conforme visto acima, os deslocamentos e momentos fletores são fatores principais para definir o vão máximo de uma viga em balanço.

Sendo assim, existem alternativas para minimizá-los e melhorar o comportamento estrutural da viga, tais como:

• Aumento da seção transversal: Aumentar a altura ou largura da viga, pois aumenta a sua rigidez;
• Adição de reforços: como barras de aço, fibras de vidro ou carbono, pode aumentar a capacidade de carga.
• Uso de materiais mais resistentes: concreto de alta resistência ou concreto protendido;
• Distribuição de cargas: evitar concentrações de carga em pontos específicos pode ajudar a reduzir os deslocamentos;
• Implementação de contra flechas: para contrabalançar os efeitos das flechas causadas pelas cargas aplicadas.

No entanto, muitas vezes, essas alternativas tornam-se inviáveis, devido a custos elevados, limite da altura do pé direito e questões de arquitetura.

E agora? você somente tem o concreto armado na sua região? Existem outras soluções estruturais?

Bem, diante desse cenário, vamos ver mais algumas possíveis recomendações?

Dicas Extras para lidar com Viga em Balanço;

A propósito, um contrabalanço é uma técnica utilizada na engenharia estrutural para equilibrar ou compensar as forças e momentos aplicados na viga em balanço.

Logo, ele consiste em adicionar um ou mais vãos, com elementos de apoio, a fim de reduzir as deformações e os esforços resultantes.

Sendo assim, o vão interno, ao receber carga, pode contribuir para reduzir a deformação no balanço e o momento fletor negativo que normalmente seria transferido para o pilar.

Em essência, um contrabalanço gera uma força ou momento que contraria os efeitos da carga principal, e ajuda a equilibrar a estrutura e reduzir seus efeitos indesejáveis, como deflexão ou tensões elevadas.

Logo, o objetivo final é melhorar a estabilidade e o desempenho estrutural da viga em balanço, e garantir a sua segurança e durabilidade.

Elementos Estruturais Inclinados;

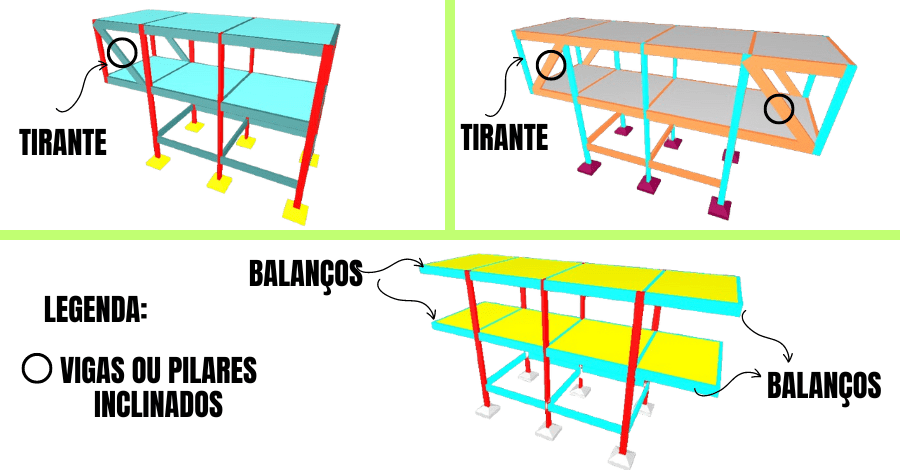
Dito isso, também vale a pena mencionar a adição de elementos estruturais extras para ajudar a suportar o balanço, Figura 6, tais como:

• Tirantes;
• Vigas Inclinadas;
• Pilares Inclinados;

Sendo assim, reduzir a carga no balanço significa diminuir o momento fletor, esforço cortante e o deslocamento, e facilitar a resolução do problema.

Logo, uma solução eficaz é usar uma viga inclinada ligada a um tirante na ponta do balanço e um pilar na outra extremidade, permitindo que eles absorvam parte da carga e diminua a carga transferida para o balanço.

No entanto, esta viga pode estar sob efeito de esforços de tração ou compressão, porém, conectada a um pilar robusto para auxiliar na estabilidade do balanço.

Portanto, o engenheiro estrutural é o responsável pela tomada de decisões nos projetos, e assim, ele sempre decide qual a melhor forma de vencer balanços em vigas, ou qualquer situação inusitada.

Por outro lado, está o arquiteto e o construtor, pois eles sempre devem chegar a um consenso comum em proveito de economia, estética e segurança.

Conclusão;

Então, vamos recapitular, as vigas em balanço são elementos bastante versáteis, e oferecem soluções estruturais que exigem muito conhecimento, atenção e experiência por parte do engenheiro,

Sendo assim, compreender seu comportamento através dos deslocamentos, momentos fletores e esforços cortantes, é essencial para projetá-las de forma eficiente, segura e econômica.

Portanto, as vigas em balanço oferecem oportunidades para a inovação arquitetônica e estrutural, com a criação de espaços expansivos, e estética atraente, pois desafiam os limites tradicionais da engenharia estrutural.

Já, os grandes desafios de uma viga em balanço, vai desde a concepção, análise estrutural, dimensionamento, e execução final na obra com chave de ouro.

Enfim, deixe as suas considerações, pois são muito bem-vindas nos comentários abaixo.